ArcCurvature

ArcCurvature[{x1,…,xn},t]

gives the curvature of the parametrized curve whose Cartesian coordinates xi are functions of t.

ArcCurvature[{x1,…,xn},t,chart]

interprets the xi as coordinates in the specified coordinate chart.

Details

  • The arc curvature is sometimes referred to as the unsigned or Frenet curvature.
  • The arc curvature of the curve 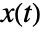in three-dimensional Euclidean space is given by (TemplateBox[{{{{x, ^, {(, ', )}}, (, t, )}, x, {{x, ^, {(, {', '}, )}}, , {(, t, )}}}}, Norm])/(TemplateBox[{{{x, ^, {(, ', )}}, (, t, )}}, Norm]^3).
  • In a general space, the arc curvature of the curve 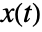is given by TemplateBox[{{{D, /, {(, {D, , t}, )}}, {{(, { , {{x, ^, {(, ', )}}, (, t, )}}, )}, /, {(, TemplateBox[{{{x, ^, {(, ', )}}, (, t, )}}, Norm], )}}}}, Norm].
  • In ArcCurvature[x,t], if x is a scalar expression, ArcCurvature gives the curvature of the parametric curve {t,x}.
  • Coordinate charts in the third argument of ArcCurvature can be specified as triples {coordsys,metric,dim} in the same way as in the first argument of CoordinateChartData. The short form in which dim is omitted may be used.

Examples

open allclose all

Basic Examples  (2)

A circle has constant curvature:

The curvature of Fermat's spiral expressed in polar coordinates:

Visualize both branches of the curve:

Scope  (5)

Curvature of loxodromes on a sphere:

A parabola has maximal curvature 2 TemplateBox[{a}, Abs] at its vertex, which decreases to 0 at infinity:

Curvature specifying metric, coordinate system, and parameters:

Parallels and meridians can be considered either curves in flat space or on the two-dimensional sphere:

As curves in three-space, they have the expected curvature inverse to their radius:

On the sphere, meridians, being geodesics, have zero curvature, but non-equatorial parallels do not:

Curvature in higher-dimensional Euclidean space:

Applications  (2)

Compute the radius of curvature of Bernoulli's lemniscate:

The Fary–Milnor theorem states that a closed curve with total curvature less than cannot be knotted. Thus, a circle, which has total curvature , cannot be a knot:

The trefoil knot must have total curvature at least , and it does:

Properties & Relations  (2)

ArcCurvature returns only a single curvature:

FrenetSerretSystem returns all curvatures in dimension :

ArcCurvature is unsigned:

Extract the two-dimensional signed curvature from FrenetSerretSystem:

Wolfram Research (2014), ArcCurvature, Wolfram Language function, https://reference.wolfram.com/language/ref/ArcCurvature.html.

Text

Wolfram Research (2014), ArcCurvature, Wolfram Language function, https://reference.wolfram.com/language/ref/ArcCurvature.html.

CMS

Wolfram Language. 2014. "ArcCurvature." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ArcCurvature.html.

APA

Wolfram Language. (2014). ArcCurvature. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ArcCurvature.html

BibTeX

@misc{reference.wolfram_2024_arccurvature, author="Wolfram Research", title="{ArcCurvature}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ArcCurvature.html}", note=[Accessed: 17-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_arccurvature, organization={Wolfram Research}, title={ArcCurvature}, year={2014}, url={https://reference.wolfram.com/language/ref/ArcCurvature.html}, note=[Accessed: 17-December-2024 ]}