AsymptoticIntegrate

AsymptoticIntegrate[f,x,xx0]

computes an asymptotic approximation of the indefinite integral for x centered at x0.

AsymptoticIntegrate[f,{x,a,b},αα0]

computes an asymptotic approximation of the definite integral for α centered at α0.

AsymptoticIntegrate[f,…,{ξ,ξ0,n}]

computes the asymptotic approximation to order n.

Details and Options

  • Asymptotic approximations to integrals are also known as asymptotic expansions and perturbation expansions. They are also known by specific methods to compute some of them, such as Laplace's method, method of stationary phase and method of steepest descent, etc.
  • Asymptotic approximations are typically used to solve problems for which no exact solution can be found or to get simpler answers for computation, comparison and interpretation.
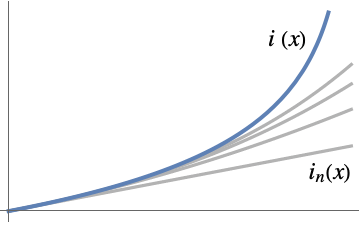
  • AsymptoticIntegrate[f,…,xx0] computes the leading term in an asymptotic expansion for the integral of f. Use SeriesTermGoal to specify more terms.
  • If the exact result is g[x] and the asymptotic approximation of order n at x0 is gn[x], then AsymptoticLess[g[x]-gn[x],gn[x]-gn-1[x],xx0] or g[x]-gn[x]∈o[gn[x]-gn-1[x]] as xx0.
  • The asymptotic approximation gn[x] is often given as a sum gn[x]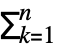αkϕk[x], where {ϕ1[x],…,ϕn[x]} is an asymptotic scale ϕ1[x]≻ϕ2[x]≻⋯>ϕn[x] as xx0. Then AsymptoticLess[g[x]-gn[x],ϕn[x],xx0] or g[x]-gn[x]∈o[ϕn[x]] as xx0.
  • Common asymptotic scales include:
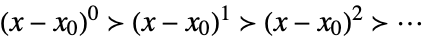
  • Taylor scale when xx0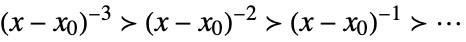
    Laurent scale when xx0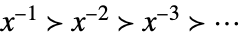
    Laurent scale when x±∞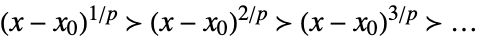
    Puiseux scale when xx0
  • The scales used to express the asymptotic approximation are automatically inferred from the problem and can often include more exotic scales.
  • The center x0 can be any finite or infinite real or complex number.
  • The order n must be a positive integer and specifies order of approximation for the asymptotic solution. It is not related to polynomial degree.
  • The following options can be given:
  • AccuracyGoalAutomaticdigits of absolute accuracy sought
    Assumptions$Assumptionsassumptions to make about parameters
    GenerateConditionsAutomaticwhether to generate answers that involve conditions on parameters
    GeneratedParameters Nonehow to name generated parameters
    MethodAutomaticmethod to use
    PerformanceGoal$PerformanceGoalaspects of performance to optimize
    PrecisionGoalAutomaticdigits of precision sought
    SeriesTermGoalAutomaticnumber of terms in the approximation
    WorkingPrecisionAutomaticthe precision used in internal computations
  • Possible settings for PerformanceGoal include $PerformanceGoal, "Quality" and "Speed". With the "Quality" setting, AsymptoticIntegrate typically solves more problems or produces simpler results, but it potentially uses more time and memory.

Examples

open allclose all

Basic Examples  (3)

Compute a leading asymptotic approximation for an integral:

Compute an asymptotic expansion for an integral:

Compare with an expansion of the exact result:

Obtain the leading term in the expansion for a Gaussian integral:

Compute the required term:

Compare with the result from a numerical approximation:

Scope  (21)

Indefinite Integrals  (3)

Compute an asymptotic expansion for a trigonometric integral about x=0:

Compare with the result given by Integrate:

Asymptotic expansion for a power tower integral about x=0:

Estimate the value at a point:

Compare with the value given by NIntegrate:

Compute an asymptotic expansion of an indefinite integral with respect to a parameter:

Exponential Integrals  (6)

Compute an asymptotic expansion for a Laplace transform integral:

Compare with the result given by LaplaceTransform:

Define a function with a Gaussian kernel having a maximum at t=-1:

Compute the leading term in the asymptotic approximation for the integral over {0,2}:

Compare the result with a numerical approximation:

Define a function with a Gaussian kernel having a maximum at t=0:

Compute an asymptotic approximation for the integral over {0,2}:

Compare the result with a numerical approximation:

Define a function with an exponential kernel having a maximum at t=1:

Compute the leading term in the asymptotic approximation for the integral over {1,2}:

Compare the result with a numerical approximation:

Define a function with an exponential kernel having a maximum at t=1:

Compute the leading term in the asymptotic approximation for the integral over {0,3}:

Compare the result with a numerical approximation:

Define a function with an exponential kernel having a maximum at t=π/2:

Compute the leading term in the asymptotic approximation for the integral over {0,3}:

Compare the result with a numerical approximation:

Oscillatory Integrals  (4)

Compute an asymptotic expansion for a Fourier-type integral on :

Find the leading-term approximation for an complex oscillatory integral on :

Compute the required approximation:

Compare with a numerical approximation:

Find the leading-term approximation for a real oscillatory integral involving Sin:

Compute the leading term:

Compare with a numerical approximation:

Compute an asymptotic expansion for a real oscillatory integral involving Cos:

Compute the expansion with two terms:

Compare with a numerical approximation:

General Definite Integrals  (4)

Compute an asymptotic expansion for the integral of a rational function at x=0:

Compare with the result given by Integrate:

Asymptotic expansion for a trigonometric integral at x=π/2:

Compare with the result given by Integrate:

Asymptotic expansion for a complete elliptic integral at x=0:

Compare with the result given by Integrate:

Asymptotic expansion for an integral at x=-Infinity:

Compare with a numerical approximation:

Transform Integrals  (4)

Asymptotic expansion for the Laplace transform of a function:

Compare with a series expansion of the exact result using LaplaceTransform:

Asymptotic expansion for the Mellin transform of a function:

Compare with a series expansion of the exact result using MellinTransform:

Asymptotic expansion for the Fourier cosine transform of a function:

Compare with a series expansion of the exact result using FourierCosTransform:

Asymptotic expansion for the Fourier sine transform of a function:

Compare with a series expansion of the exact result using FourierSinTransform:

Options  (1)

GeneratedParameters  (1)

Generate an arbitrary constant for an indefinite integral:

The default value for the arbitrary constant is 0:

Applications  (7)

Obtain an asymptotic expansion for a definite integral:

Compare with a numerical approximation:

Improve the asymptotic approximation by increasing the number of terms:

Find the area under the curve of from to :

Find the area for a specific value of :

Compute the volume enclosed when for is rotated about the axis:

Find the volume for a specific value of :

Visualize the solid:

Define an asymptotic version of LaplaceTransform:

Use it to compute the asymptotic Laplace transform of a periodic function:

Plot the result:

Compare with a numerical approximation:

Compute the asymptotic mean for a ProbabilityDistribution with domain :

Normalize the PDF:

Plot the PDF:

Define the asymptotic mean:

Compute the asymptotic mean for the given distribution:

Compare with an expansion of the exact result:

Obtain an asymptotic expansion for the integral representation of BesselJ:

Compare with numerical values of the Bessel function:

Compute an asymptotic approximation for an oscillatory integral:

Compare the result with a numerical approximation:

Properties & Relations  (4)

AsymptoticIntegrate computes the integral up to a given order:

Use Integrate to compute the integral in closed form:

Use NIntegrate to compute a numerical approximation:

Use AsymptoticExpectation to compute an asymptotic expectation:

Obtain the same result using AsymptoticIntegrate:

Possible Issues  (1)

The expansion returned for this example has fewer than four terms:

The missing terms are present in the expansion for a more general integral:

Wolfram Research (2018), AsymptoticIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/AsymptoticIntegrate.html (updated 2020).

Text

Wolfram Research (2018), AsymptoticIntegrate, Wolfram Language function, https://reference.wolfram.com/language/ref/AsymptoticIntegrate.html (updated 2020).

CMS

Wolfram Language. 2018. "AsymptoticIntegrate." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/AsymptoticIntegrate.html.

APA

Wolfram Language. (2018). AsymptoticIntegrate. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AsymptoticIntegrate.html

BibTeX

@misc{reference.wolfram_2024_asymptoticintegrate, author="Wolfram Research", title="{AsymptoticIntegrate}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/AsymptoticIntegrate.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_asymptoticintegrate, organization={Wolfram Research}, title={AsymptoticIntegrate}, year={2020}, url={https://reference.wolfram.com/language/ref/AsymptoticIntegrate.html}, note=[Accessed: 17-November-2024 ]}