EdgeCycleMatrix

EdgeCycleMatrix[g]

gives the edge cycle matrix of a graph g.

EdgeCycleMatrix[{vw,…}]

uses rules vw to specify the graph g.

Details

  • EdgeCycleMatrix is also known as tie-set matrix or loop matrix.
  • EdgeCycleMatrix returns a matrix cij where each row corresponds to a cycle i in the graph g, and each column corresponds to an edge ej.
  • For an undirected graph, cij is 1 if edge ej is part of cycle i and zero otherwise.
  • For a directed graph, cij is 1 if edge ej is part of cycle i, -1 if edge ej in reverse direction is part of cycle i, and zero otherwise.
  • Edge ej is the edge at position j in EdgeList[g], and the index j for an edge ej can be found from EdgeIndex[g,ej].
  • EdgeCycleMatrix gives a basis for all the cycles in the graph g.
  • EdgeCycleMatrix works with undirected graphs, directed graphs, multigraphs, and mixed graphs.

Background & Context

  • EdgeCycleMatrix returns a matrix cij in which each row corresponds to a cycle i in a graph and each column corresponds to an edge ej. An edge cycle matrix is determined by the incidences of edges and cycles in a graph, and cycles in an edge cycle matrix form a cycle basis of a graph. Cycle bases are useful in the study of chemical graphs, to generate large cycle families, and to compute voltage or current in a circuit. Edge cycle matrices are also known as tie-set or loop matrices.
  • For an undirected graph, cij is 1 if edge ej is part of cycle i and zero otherwise. For a directed graph, cij is 1 if edge ej is part of cycle i, 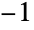if edge ej in reverse direction is part of cycle i, and zero otherwise.
  • FindFundamentalCycles is a related function that can be used to return a list of fundamental cycles of a graph.

Examples

open allclose all

Basic Examples  (2)

Find the edge cycle matrix of a graph:

Obtain a cycle basis of a graph:

Show the cycles:

Scope  (6)

EdgeCycleMatrix works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

Use rules to specify the graph:

EdgeCycleMatrix works with large graphs:

Applications  (1)

Obtain a cycle basis of a graph:

Build all simple cycles:

Properties & Relations  (3)

Use EdgeList to obtain a cycle representation:

A connected graph with n vertices and m edges:

Has an edge cycle matrix of dimensions (m-n+1)×m:

Compute the EdgeCycleMatrix from the IncidenceMatrix:

Compare with EdgeCycleMatrix:

Wolfram Research (2014), EdgeCycleMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/EdgeCycleMatrix.html (updated 2015).

Text

Wolfram Research (2014), EdgeCycleMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/EdgeCycleMatrix.html (updated 2015).

CMS

Wolfram Language. 2014. "EdgeCycleMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/EdgeCycleMatrix.html.

APA

Wolfram Language. (2014). EdgeCycleMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EdgeCycleMatrix.html

BibTeX

@misc{reference.wolfram_2024_edgecyclematrix, author="Wolfram Research", title="{EdgeCycleMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/EdgeCycleMatrix.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_edgecyclematrix, organization={Wolfram Research}, title={EdgeCycleMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/EdgeCycleMatrix.html}, note=[Accessed: 30-December-2024 ]}