IncidenceMatrix

IncidenceMatrix[g]

gives the vertex-edge incidence matrix of the graph g.

IncidenceMatrix[{vw,…}]

uses rules vw to specify the graph g.

Details

  • IncidenceMatrix is also known as the vertex-edge incidence matrix.
  • IncidenceMatrix returns a SparseArray object, which can be converted to an ordinary matrix using Normal.
  • The incidence matrix for a graph with vertices {v1,…,vn} and edges {e1,…,em} is an 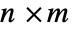matrix with entries aij given by:
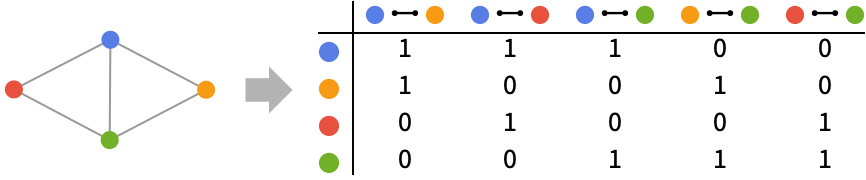
  • 0vi is not incident to ej
    1ej=vivk, ej=vkvi, or ej=vkvi
    -1ej=vivk
    2ej=vivi
    -2ej=vivi
  • The vertices vi are assumed to be in the order given by VertexList[g] and the edges ej are assumed to be in the order given by EdgeList[g].

Examples

open allclose all

Basic Examples  (2)

The incidence matrix of an undirected graph:

The incidence matrix of a directed graph:

Scope  (5)

The incidence matrix of an undirected graph has no negative entries:

The sum of the entries in any column is 2:

The incidence matrix of a directed graph has some negative entries:

If there are no self-loops, the sum of the entries in any column is 0:

The incidence matrix of a graph with self-loops has some entries equal to 2:

Use rules to specify the graph:

IncidenceMatrix works with large graphs:

Use MatrixPlot to visualize the matrix:

Properties & Relations  (9)

Rows and columns correspond to VertexList and EdgeList order:

The ^(th) row gives all edge indices incident to the ^(th) vertex:

The first vertex is incident to edges 2, 3, and 4:

The ^(th) column gives all vertex indices incident to the ^(th) edge:

The second edge is incident to vertices 1 and 3:

Use VertexIndex and EdgeIndex to find the indices for vertices and edges:

The incidence matrix can tell whether a vertex and edge are incident:

The incidence matrix for a directed graph indicates the source vertex by and the target vertex by :

Compute the oriented incidence matrix for an undirected graph using DirectedGraph:

The oriented incidence matrix using a random orientation:

The dimensions of the incidence matrix are given by VertexCount and EdgeCount:

Use IncidenceGraph to construct a graph from an incidence matrix:

The adjacency matrix of a line graph can be computed by its IncidenceMatrix:

Wolfram Research (2010), IncidenceMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/IncidenceMatrix.html (updated 2015).

Text

Wolfram Research (2010), IncidenceMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/IncidenceMatrix.html (updated 2015).

CMS

Wolfram Language. 2010. "IncidenceMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/IncidenceMatrix.html.

APA

Wolfram Language. (2010). IncidenceMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/IncidenceMatrix.html

BibTeX

@misc{reference.wolfram_2024_incidencematrix, author="Wolfram Research", title="{IncidenceMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/IncidenceMatrix.html}", note=[Accessed: 12-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_incidencematrix, organization={Wolfram Research}, title={IncidenceMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/IncidenceMatrix.html}, note=[Accessed: 12-November-2024 ]}