HilbertCurve

HilbertCurve[n]

gives the line segments representing the n^(th)-step Hilbert curve.

HilbertCurve[n,d]

gives the n^(th)-step Hilbert curve in dimension d.

Details and Options

  • HilbertCurve is also known as Hilbert space-filling curve.
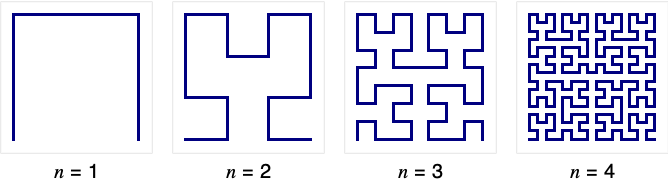
  • HilbertCurve[n] returns a Line primitive corresponding to a path that starts at {0,0}, then joins all integer points in the 2n-1 by 2n-1 square, and ends at {2n-1,0}. »
  • HilbertCurve takes a DataRange option that can be used to specify the range the coordinates should be assumed to occupy.

Examples

open allclose all

Basic Examples  (2)

A 2D Hilbert curve:

Lengths of the approximations to the Hilbert curve:

The formula:

Visualize the Hilbert curve in 2D with splines:

Scope  (8)

Curve Specification  (4)

A 2D Hilbert curve:

A 3D Hilbert curve:

An D Hilbert curve:

The ^(th) approximation of the Hilbert curve:

Curve Styling  (4)

Hilbert curves with different thicknesses:

Thickness in scaled size:

Thickness in printer's points:

Dashed curves:

Colored curves:

Generalizations & Extensions  (2)

Hilbert curve in 4D:

Hilbert curve in D:

Options  (1)

DataRange  (1)

DataRange allows you to specify the range of mesh coordinates to generate:

Specify a different range:

Applications  (4)

HilbertCurve is constructed recursively by transforming cups into four cups linked together by lines:

Next iteration:

Visualize the Hilbert curve in 2D:

With splines:

In 3D:

With tubes:

Build a polygon from the Hilbert curve:

Apply a Hilbert curve texture to a surface:

Properties & Relations  (3)

HilbertCurve consists of lines:

Find the perimeter of the 2D Hilbert curve:

3D Hilbert curve:

DataRangerange is equivalent to using RescalingTransform[{…},range]:

Use RescalingTransform:

Possible Issues  (2)

By default, the coordinates of the Hilbert curve are not in the unit square:

Using DataRange to generate the Hilbert curve in the unit square:

HilbertCurve can be too large to generate:

Neat Examples  (1)

Traversal animations:

Wolfram Research (2017), HilbertCurve, Wolfram Language function, https://reference.wolfram.com/language/ref/HilbertCurve.html.

Text

Wolfram Research (2017), HilbertCurve, Wolfram Language function, https://reference.wolfram.com/language/ref/HilbertCurve.html.

CMS

Wolfram Language. 2017. "HilbertCurve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HilbertCurve.html.

APA

Wolfram Language. (2017). HilbertCurve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HilbertCurve.html

BibTeX

@misc{reference.wolfram_2025_hilbertcurve, author="Wolfram Research", title="{HilbertCurve}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/HilbertCurve.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_hilbertcurve, organization={Wolfram Research}, title={HilbertCurve}, year={2017}, url={https://reference.wolfram.com/language/ref/HilbertCurve.html}, note=[Accessed: 21-February-2025 ]}