represents the sporadic simple Janko group ![]() .
.


JankoGroupJ2
represents the sporadic simple Janko group ![]() .
.
Details
- By default, JankoGroupJ2[] is represented as a permutation group acting on points {1,…,100}.
- This group is also known as the Hall–Janko group or Hall–Janko–Wales group.
Background & Context
- JankoGroupJ2[] represents the Janko group
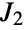 , which is a group of order
, which is a group of order ![TemplateBox[{2, 7}, Superscript].TemplateBox[{3, 3}, Superscript].TemplateBox[{5, 2}, Superscript].7 TemplateBox[{2, 7}, Superscript].TemplateBox[{3, 3}, Superscript].TemplateBox[{5, 2}, Superscript].7](Files/JankoGroupJ2.en/3.png) . It is one of the 26 sporadic simple groups of finite order. The default representation of JankoGroupJ2 is as a permutation group on the symbols
. It is one of the 26 sporadic simple groups of finite order. The default representation of JankoGroupJ2 is as a permutation group on the symbols 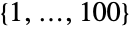 having two generators.
having two generators.  may also be referred to as the Hall–Janko group (denoted
may also be referred to as the Hall–Janko group (denoted 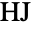 ) or the Hall–Janko–Wales group.
) or the Hall–Janko–Wales group. - The Janko group
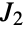 is the fifth smallest of the sporadic finite simple groups. It was discovered (along with JankoGroupJ1 and JankoGroupJ3) by mathematician Zvonimir Janko in the mid 1900s, making these groups tied for second in chronological order of discovery among sporadic groups. JankoGroupJ2 is the unique Janko group occurring as a subquotient of the monster group. In addition to its permutation representation,
is the fifth smallest of the sporadic finite simple groups. It was discovered (along with JankoGroupJ1 and JankoGroupJ3) by mathematician Zvonimir Janko in the mid 1900s, making these groups tied for second in chronological order of discovery among sporadic groups. JankoGroupJ2 is the unique Janko group occurring as a subquotient of the monster group. In addition to its permutation representation, 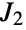 can be defined in terms of generators and relations as
can be defined in terms of generators and relations as 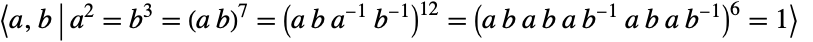 . It is contained in the Conway group
. It is contained in the Conway group 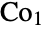 , thus making it the only Janko group to be part of the "second generation" of sporadic simple groups. Along with the other sporadic simple groups, the Janko groups played a foundational role in the monumental (and complete) classification of finite simple groups.
, thus making it the only Janko group to be part of the "second generation" of sporadic simple groups. Along with the other sporadic simple groups, the Janko groups played a foundational role in the monumental (and complete) classification of finite simple groups. - The usual group theoretic functions may be applied to JankoGroupJ2[], including GroupOrder, GroupGenerators, GroupElements and so on. A number of precomputed properties of the Janko group
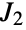 are available via FiniteGroupData[{"Janko",2},"prop"].
are available via FiniteGroupData[{"Janko",2},"prop"]. - JankoGroupJ2 is related to a number of other symbols. JankoGroupJ2 is one of the seven groups (along with the Conway groups ConwayGroupCo1, ConwayGroupCo2 and ConwayGroupCo3, and together with HigmanSimsGroupHS, McLaughlinGroupMcL and SuzukiGroupSuz) collectively referred to as the "second generation" of sporadic finite simple groups. It is also one of 20 so-called "happy" sporadic groups, which all appear as a subquotient of the monster group.
Tech Notes
Related Guides
History
Text
Wolfram Research (2010), JankoGroupJ2, Wolfram Language function, https://reference.wolfram.com/language/ref/JankoGroupJ2.html.
CMS
Wolfram Language. 2010. "JankoGroupJ2." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/JankoGroupJ2.html.
APA
Wolfram Language. (2010). JankoGroupJ2. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/JankoGroupJ2.html
BibTeX
@misc{reference.wolfram_2025_jankogroupj2, author="Wolfram Research", title="{JankoGroupJ2}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/JankoGroupJ2.html}", note=[Accessed: 15-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_jankogroupj2, organization={Wolfram Research}, title={JankoGroupJ2}, year={2010}, url={https://reference.wolfram.com/language/ref/JankoGroupJ2.html}, note=[Accessed: 15-January-2026]}