MatrixFunction

MatrixFunction[f,m]

gives the matrix generated by the scalar function f at the matrix argument m.

Details and Options

  • A matrix function transforms a matrix to another matrix. For convergent power series, MatrixFunction[f,m] effectively evaluates the power series for the function f with ordinary powers replaced by matrix powers. »
  • The function f should be a unary differentiable or symbolic function.
  • MatrixFunction works only on square matrices. It applies the Schur–Parlett method for inexact matrices and Jordan decomposition for exact or symbolic matrices.
  • MatrixFunction can be used on SparseArray objects and structured arrays.
  • A Method option can be given, with possible explicit settings:
  • "Jordan"Jordan decomposition
    "Schur"Schur decomposition with block Parlett recursion
  • The "Schur" method can be specified with method options mopts by Method->{"Schur",mopts}. The following method options can be given:
  • "Balanced"Falsewhether to balance the input matrix before doing the Schur decomposition
    "BlockSeparationDelta"Automaticmaximum separation between adjacent eigenvalues in a single Parlett block

Examples

open allclose all

Basic Examples  (3)

Compute the square root of a symbolic matrix:

Verify that it is, indeed, a square root:

Note that this is different from simply computing the square root of each entry:

Compute the logarithm of a 3×3 matrix m:

Verify that the exponential of the result is the original matrix:

Compute a matrix polynomial, specifying the polynomial as a pure function:

Scope  (11)

Basic Uses  (7)

Compute the matrix sine and cosine of a machine-precision matrix:

Test the matrix identity :

Compute the matrix sine for a complex matrix:

Compute the square root of an exact matrix:

Use 20-digit-precision arithmetic to compute the matrix function of a logarithm of a polynomial:

Compute the matrix sine of a symbolic diagonal matrix:

Compute the matrix tangent of a symbolic non-diagonal matrix:

Compute a matrix function with a symbolic scalar function:

Use a symbolic matrix with a symbolic scalar function:

Applying a function to a machine-precision matrix is efficient:

Special Matrices  (4)

Computing a matrix function with a sparse matrix generally produces a normal matrix:

Compute a matrix polynomial of a structured array:

Applying a matrix function to an identity matrix only changes the value of the diagonal elements:

More generally, a function of any diagonal matrix is the function applied to its diagonal elements:

Compute the square of HilbertMatrix to 20-digit precision:

Options  (4)

Method  (4)

The method "Jordan" can work with exact and inexact matrices:

The method "Schur" works only with inexact (machine- and arbitrary-precision) matrices:

If many eigenvalues are very close, they are put in a diagonal-block submatrix, which may become large; computations are then more expensive and convergence may be slow:

A smaller value for "BlockSeparationDelta" reduces the diagonal block size and also speeds convergence:

But the result may be much less accurate:

When an input matrix is poorly balanced (containing terms of very different magnitudes), balancing may improve the result:

Applications  (5)

Find the second inverse matrix power applied to a particular vector:

This is a more efficient way of computing :

Show that a matrix is a root of its characteristic polynomial:

The solution of , , for a scalar symbol is given with:

If is a matrix, the solution can be computed using matrix functions in the scalar solution:

Find the matrix that satisfies :

Confirm the formula 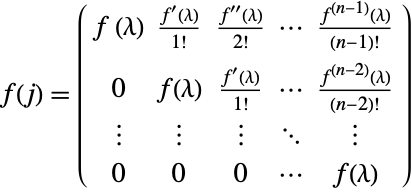for a Jordan matrix consisting of a single chain for the following matrix :

Properties & Relations  (11)

Using the function 1& returns an identity matrix:

Using the function 1/#& is the same as using Inverse:

Using a function that is a power is equivalent to using MatrixPower:

MatrixFunction[Exp,m] is essentially equivalent to MatrixExp[m]:

MatrixFunction effectively uses the power series, with Power replaced by MatrixPower:

Just as , MatrixExp[MatrixFunction[Log,m]] equals m:

If m is diagonal, MatrixFunction[f,m] merely applies f to each element of the diagonal of m:

If m is upper triangular, MatrixFunction[f,m] is also upper triangular:

The analogous statement holds for lower-triangular matrices:

If is diagonalizable with and the eigenvectors are well conditioned, then :

can be computed from the JordanDecomposition as v.f(j).TemplateBox[{v}, Inverse]:

Moreover, is zero except in upper-triangular blocks delineated by s in the superdiagonal:

A matrix is a root of its characteristic polynomial:

Possible Issues  (4)

The scalar function can have symbolic derivatives for exact or symbolic matrices:

Compare with this example:

MatrixFunction does not work with non-differentiable functions such as Abs:

It will return a matrix function for an exact input matrix, but the result is meaningless because Abs does not have a first or second derivative:

MatrixFunction does not return a result when the scalar function or any of its initial derivatives are not defined at matrix eigenvalues:

The scalar function f has poles (singularities) at 1, 2, and 3:

If a scalar function is not analytic and a matrix eigenvalue is close to a function pole, the resulting matrix is usually incorrect:

Neat Examples  (1)

Wolfram Research (2012), MatrixFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/MatrixFunction.html (updated 2014).

Text

Wolfram Research (2012), MatrixFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/MatrixFunction.html (updated 2014).

CMS

Wolfram Language. 2012. "MatrixFunction." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/MatrixFunction.html.

APA

Wolfram Language. (2012). MatrixFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MatrixFunction.html

BibTeX

@misc{reference.wolfram_2024_matrixfunction, author="Wolfram Research", title="{MatrixFunction}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/MatrixFunction.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_matrixfunction, organization={Wolfram Research}, title={MatrixFunction}, year={2014}, url={https://reference.wolfram.com/language/ref/MatrixFunction.html}, note=[Accessed: 21-November-2024 ]}