NetPortGradient["port"]
represents the gradient of the output of a net with respect to the value of the specified input port.
NetPortGradient["param"]
represents the gradient of the output with respect to a learned parameter named param.
NetPortGradient[{layer1,layer2,…,"param"}]
represents the gradient with respect to a parameter at a specific position in a net.
represents the gradients with respect to all inputs and parameters.


NetPortGradient
NetPortGradient["port"]
represents the gradient of the output of a net with respect to the value of the specified input port.
NetPortGradient["param"]
represents the gradient of the output with respect to a learned parameter named param.
NetPortGradient[{layer1,layer2,…,"param"}]
represents the gradient with respect to a parameter at a specific position in a net.
represents the gradients with respect to all inputs and parameters.
Details

- NetPortGradient is typically used to calculate gradients with respect to both learned parameters of a network and inputs to the network.
- net[data,NetPortGradient[iport]] can be used to obtain the gradient with respect to the input port iport for a net applied to the specified data.
- net[<|…,NetPortGradient[oport]ograd|>,NetPortGradient[iport]] can be used to impose a gradient at an output port oport that will be backpropogated to calculate the gradient at iport.
- For a net with a single scalar output port, the gradient returned when using NetPortGradient is the gradient in the ordinary mathematical sense: for a net computing
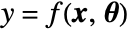 , where
, where 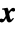 is the array whose gradient is being calculated and
is the array whose gradient is being calculated and 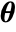 represents all other arrays, the gradient is an array of the same rank as
represents all other arrays, the gradient is an array of the same rank as 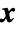 , whose components are given by
, whose components are given by 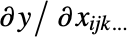 . Intuitively, the gradient at a specific value of
. Intuitively, the gradient at a specific value of 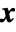 is the "best direction" in which to perturb
is the "best direction" in which to perturb 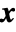 if the goal is to increase
if the goal is to increase 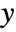 , where the magnitude of the gradient is proportional to the sensitivity of
, where the magnitude of the gradient is proportional to the sensitivity of 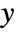 to changes in
to changes in 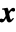 .
. - For a net with vector or array outputs, the gradient returned when using NetPortGradient is the ordinary gradient of the scalar sum of all outputs. Imposing a gradient at the output using the syntax <|…,NetPortGradient[oport]ograd|> is equivalent to replacing this scalar sum with a dot product between the output and ograd.
- Using NetPortGradient to calculate the gradient with respect to the learned parameters of the net will return the sum of the gradient over the input batch.
Examples
open all close allBasic Examples (3)
Create an elementwise layer and return the derivative of the input with respect to the output:
The derivative for negative values is zero:
Randomly initialize a LinearLayer and return the derivative of the output with respect to the input for a specific input value:
Compare with a naive numeric calculation:
Create a binary cross-entropy loss layer:
Evaluate the loss for an input and target:
The derivative of the input is negative because the input is below the target (increasing the input would lower the loss):
The derivative of the input is positive when the input is above the target:
Scope (2)
Randomly initialize a chain of linear layers:
Return the derivative of the output with respect to the weights and biases of the first layer, for a specific input value:
Calculate the gradient at the input:
Impose a gradient at the output:
Compute all the gradients in one call:
Chain a PoolingLayer to a PartLayer that extracts the red color channel:
Calculate the input gradient on a test image:
Visualize the gradient, which shows that the total output of this net would only be increased if pixels are reddened that are far from the existing red or white areas:
Properties & Relations (1)
Tech Notes
Related Guides
Text
Wolfram Research (2017), NetPortGradient, Wolfram Language function, https://reference.wolfram.com/language/ref/NetPortGradient.html (updated 2022).
CMS
Wolfram Language. 2017. "NetPortGradient." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/NetPortGradient.html.
APA
Wolfram Language. (2017). NetPortGradient. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/NetPortGradient.html
BibTeX
@misc{reference.wolfram_2025_netportgradient, author="Wolfram Research", title="{NetPortGradient}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/NetPortGradient.html}", note=[Accessed: 15-December-2025]}
BibLaTeX
@online{reference.wolfram_2025_netportgradient, organization={Wolfram Research}, title={NetPortGradient}, year={2022}, url={https://reference.wolfram.com/language/ref/NetPortGradient.html}, note=[Accessed: 15-December-2025]}