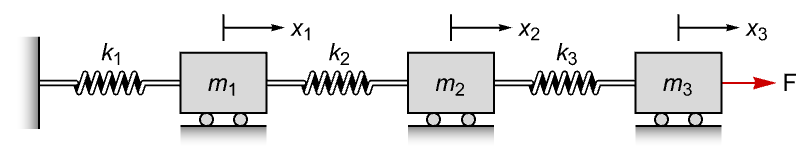
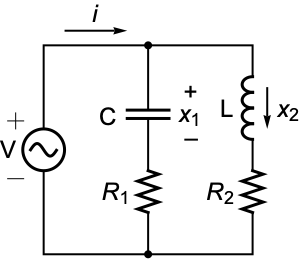
ObservableModelQ

ObservableModelQ[sys]

gives True if the system sys is observable, and False otherwise.

ObservableModelQ[{sys,sub}]

gives True if the subsystem sub is observable.

Details and Options

  • A state-space model is said to be observable at 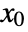if the trajectory of the model from 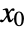is distinguishable from that of another state in its neighborhood in finite time.
  • The system sys can be a standard or descriptor StateSpaceModel or AffineStateSpaceModel.
  • The following subsystems sub can be specified:
  • Allwhole system
    "Fast"fast subsystem
    "Slow"slow subsystem
    "Unstable"unstable subsystem
    {λ1,…}subsystem with eigenmodes 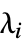lambda_(i)
  • The "Fast" and "Slow" subsystems primarily apply to descriptor state-space models as described in KroneckerModelDecomposition.
  • The eigenmodes λi are described in JordanModelDecomposition.
  • ObservableModelQ accepts a Method option with the following settings:
  • Automaticautomatically choose the appropriate test
    "Distribution"use observability distribution's rank
    "Gramian"use observability Gramian's rank or positive definiteness
    "Matrix"use observability matrix's rank
    "PBH"use Popov–Belevitch–Hautus rank test

Examples

open allclose all

Basic Examples  (2)

An observable system:

An unobservable system, since the second state is not observable:

Scope  (6)

Test the observability of a system with approximate coefficients:

Exact coefficients:

Symbolic coefficients:

Multiple-output system:

Discrete-time system:

A descriptor system:

Observability is equivalent to observability of both slow and fast modes (C-observability):

Test observability of individual eigenmodes:

The system is unobservable because of eigenmode :

This can be seen in the Jordan form, where there is no way to observe the second state:

Test observability of an AffineStateSpaceModel:

If an operating point is given, observability at is tested:

The system is observable at a generic point:

Options  (6)

Method  (6)

By default, the observability matrix is used for exact and symbolic systems:

The system is observable if the ObservabilityMatrix has full rank:

The observability Gramian is used for stable numeric systems:

The system is observable if the ObservabilityGramian has full rank:

For the observability Gramian, this is equivalent to it being positive definite:

The PBH rank test is used for all other numeric systems:

The system is observable because has full rank for all :

The observability codistribution is used for input-linear systems:

For linear systems, the tests based on the observability matrix and codistribution are equivalent:

Observability of the linearized system implies observability of the input-linear system:

The matrix test for input-linear systems uses the "Matrix" method for the linearized system:

Applications  (2)

The positions and velocities of all three masses can be estimated from the measurement of :

An electric circuit with the capacitor voltage and inductor current as states and current as measurement:

In general, the system is observable:

However, if , it is not observable:

Properties & Relations  (6)

A diagonal system is observable, assuming and :

With , there is no way to observe the first state:

With , the second state cannot be observed directly, but indirectly from the first state:

With , the first state cannot be observed directly or indirectly from the second state:

Use JordanModelDecomposition to compute the preceding canonical state-space representation:

Compute the observability of each mode using the "PBH" test:

For descriptor systems, KroneckerModelDecomposition is the generalization of the diagonal form:

Determine the observability of the slow subsystem from its structure:

Compute it using the original system:

Determine the observability of the fast subsystem from its structure:

Compute it using the original system:

If the descriptor matrix of a StateSpaceModel has full rank, there is no fast subsystem:

Hence the complete controllability of the system can be evaluated from the slow subsystem:

For AffineStateSpaceModel, the nonlinearities in the input vectors aid observability:

The system with a linear input vector is not observable:

Unobservable systems have indistinguishable initial states:

The two initial states and produce indistinguishable outputs:

Possible Issues  (1)

The Gramian method is not reliable for systems that are not asymptotically stable:

Wolfram Research (2010), ObservableModelQ, Wolfram Language function, https://reference.wolfram.com/language/ref/ObservableModelQ.html (updated 2014).

Text

Wolfram Research (2010), ObservableModelQ, Wolfram Language function, https://reference.wolfram.com/language/ref/ObservableModelQ.html (updated 2014).

CMS

Wolfram Language. 2010. "ObservableModelQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ObservableModelQ.html.

APA

Wolfram Language. (2010). ObservableModelQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ObservableModelQ.html

BibTeX

@misc{reference.wolfram_2024_observablemodelq, author="Wolfram Research", title="{ObservableModelQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ObservableModelQ.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_observablemodelq, organization={Wolfram Research}, title={ObservableModelQ}, year={2014}, url={https://reference.wolfram.com/language/ref/ObservableModelQ.html}, note=[Accessed: 17-November-2024 ]}