RiemannR

RiemannR[x]

gives the Riemann prime counting function TemplateBox[{x}, RiemannR].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • For 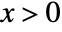, the Riemann prime counting function is given by TemplateBox[{x}, RiemannR]=sum_n^inftyTemplateBox[{n}, MoebiusMu] TemplateBox[{{x, ^, {(, {1, /, n}, )}}}, LogIntegral]/n.
  • RiemannR[z] has a branch cut discontinuity in the complex z plane running from 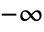to .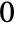
  • RiemannR can be evaluated to arbitrary numerical precision.
  • RiemannR automatically threads over lists.

Examples

open allclose all

Basic Examples  (2)

Evaluate numerically:

Compare the behavior of RiemannR with the prime counting function TemplateBox[{x}, PrimePi]:

Scope  (6)

Evaluate for complex arguments:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Simple exact values are generated automatically:

RiemannR threads element-wise over lists:

TraditionalForm formatting:

Applications  (1)

The behavior of RiemannR near the origin:

The largest root of the Riemann prime counting function, which solves a problem originally posed by Waldvogel:

The second largest root:

Wolfram Research (2008), RiemannR, Wolfram Language function, https://reference.wolfram.com/language/ref/RiemannR.html.

Text

Wolfram Research (2008), RiemannR, Wolfram Language function, https://reference.wolfram.com/language/ref/RiemannR.html.

CMS

Wolfram Language. 2008. "RiemannR." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/RiemannR.html.

APA

Wolfram Language. (2008). RiemannR. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RiemannR.html

BibTeX

@misc{reference.wolfram_2024_riemannr, author="Wolfram Research", title="{RiemannR}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/RiemannR.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_riemannr, organization={Wolfram Research}, title={RiemannR}, year={2008}, url={https://reference.wolfram.com/language/ref/RiemannR.html}, note=[Accessed: 21-December-2024 ]}