StateTransformationLinearize

StateTransformationLinearize[asys]

linearizes the AffineStateSpaceModel asys by state transformation.

StateTransformationLinearize[asys,{z,lform}]

specifies the new states z and form of linearization lform.

StateTransformationLinearize[asys,…,"prop"]

computes the property "prop".

Details and Options

  • StateTransformationLinearize attempts to transform an affine system to a linear one so that linear control techniques can be used on the linearized dynamics.
  • Using a state transformation x->p[z], the original affine system with dynamics 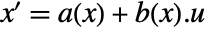and output 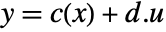gets transformed to an input-output, input-state, or state-output linear system.
  • The following forms of exact linearization lform can be used:
  • Automaticautomatically linearize
    "InputOutput",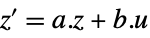
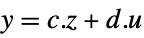
    "InputState",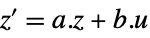
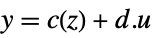
    "StateOutput",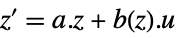
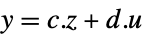
  • The Automatic setting will attempt "InputOutput", "InputState", or "StateOutput".
  • StateTransformationLinearize returns a LinearizingTransformationData object that can be used to extract detailed properties for further analysis and design.
  • Properties related to the state transformation include:
  • "InverseStateTransformation"inverse state transformation
    "StateTransformation"state transformation
    "TransformedSystem"linearized or partially linearized transformed system tsys
    "Linearization"form of linearization "lform"
  • Properties related to controller and estimator design include:
  • {"OriginalSystemController",cs}controller for asys based on controller cs designed for tsys
    {"OriginalSystemEstimator",es}estimator for asys based on estimator es designed for tsys
    {"ClosedLoopSystem",cs}closed-loop system based on the linear controller cs

Examples

open allclose all

Basic Examples  (1)

Linearize an affine system using state transformation:

The transformed system is completely linear:

Compute feedback gains for the system, using the linearized system:

The closed-loop system:

The closed-loop system is stable:

Scope  (12)

Basic Uses  (5)

Linearize an affine system:

The transformed system shows that the state-to-output dynamics have been linearized:

Explicitly obtain the type of linearization:

Specify the new state variables to use:

Specify the type of linearization to use:

The input dynamics are linear, but the output is nonlinear:

Specify the property upfront:

Multiple properties can be specified:

Specify several properties:

Input-Output Linearize  (3)

Get transformation-related properties:

Forward and inverse state transformations:

The transformed linear system:

Design controllers using exact and approximate linearization, and compare:

The transformed system:

Design a controller and observer for the linearized system:

The closed-loop system:

The simulation of the closed-loop system:

A controller based on approximate linearization, using same specifications:

Simulate the system:

Compare the responses:

Design estimators using exact and approximate linearization, and compare:

The transformed system:

The estimator for the original system:

The trajectories of the estimated states:

An estimator based on approximate linearization, using the same specification:

The trajectories of the estimated states, based on approximate linearization:

Compute the actual state trajectories:

Compare the actual and estimated trajectories of the first state:

Compare the actual and estimated trajectories of the second state:

State-Output Linearize  (2)

Get transformation-related properties:

Forward and inverse state transformations:

The transformed system with linear dynamics from state to output:

Design an estimator using exact linearization:

The transformed system:

The estimator for the original system:

The trajectories of the estimated states:

The actual state trajectories:

Compare the estimated and actual state trajectories:

Input-State Linearize  (2)

Get transformation-related properties:

Forward and inverse state transformations:

The transformed system with linear dynamics from input to state:

Design controllers using exact and approximate linearization, and compare:

The transformed system:

A controller based on exact linearization:

The closed-loop system:

The design based on approximate linearization:

The closed-loop system with feedback, based on approximate linearization:

Compare the two designs:

Properties & Relations  (4)

The transformed system is related to the input system by StateSpaceTransform:

The input-output linearized system is controllable and observable:

The state-output linearized system is observable:

The input-state linearized system is controllable:

Wolfram Research (2014), StateTransformationLinearize, Wolfram Language function, https://reference.wolfram.com/language/ref/StateTransformationLinearize.html.

Text

Wolfram Research (2014), StateTransformationLinearize, Wolfram Language function, https://reference.wolfram.com/language/ref/StateTransformationLinearize.html.

CMS

Wolfram Language. 2014. "StateTransformationLinearize." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StateTransformationLinearize.html.

APA

Wolfram Language. (2014). StateTransformationLinearize. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StateTransformationLinearize.html

BibTeX

@misc{reference.wolfram_2024_statetransformationlinearize, author="Wolfram Research", title="{StateTransformationLinearize}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/StateTransformationLinearize.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_statetransformationlinearize, organization={Wolfram Research}, title={StateTransformationLinearize}, year={2014}, url={https://reference.wolfram.com/language/ref/StateTransformationLinearize.html}, note=[Accessed: 21-November-2024 ]}