Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram Language & System Documentation Center

TitsGroupT

TitsGroupT

represents the simple Tits group .

Details

The default permutation representation of TitsGroupT[] acts on points {1,…,1600}.

Background & Context

TitsGroupT[] represents the Tits group , sometimes also denoted , which is a group of order . The default representation of TitsGroupT is as a permutation group on the symbols having two generators.
The Tits group was first introduced in the mid-1960s by mathematician Jacques Tits as the (simple) derived subgroup of the (non-simple) Ree group of Lie type. Because is not strictly a group of Lie type, it is sometimes regarded as a 27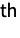 sporadic simple group. The Tits group can be realized as a maximal subgroup of the Fischer group . In addition to its default permutation representation, it can be defined in terms of generators and relations as , where .
The usual group theoretic functions may be applied to TitsGroupT[], including GroupOrder, GroupGenerators, GroupElements and so on. A number of precomputed properties of the Tits group are available via FiniteGroupData["Tits","prop"].
When considered together with the "true" sporadic finite simple groups, TitsGroupT[] is considered a "pariah" even though it occurs as a subquotient of MonsterGroupM (which is the criterion whose failure makes JankoGroupJ1, JankoGroupJ3, JankoGroupJ4, LyonsGroupLy, ONanGroupON and RudvalisGroupRu "pariahs").

Examples

Basic Examples (3)

Order of the Tits group:

Number of points moved by the generators of a permutation representation of the Tits group:

Order of a pseudorandom element of the group:

Top