Changing Coordinate Systems
Changing coordinate systems can involve two very different operations. One is recomputing coordinate values that correspond to the same point. The other is re-expressing a field in terms of new variables. The Wolfram Language provides functions to perform both these operations.
Two coordinate systems are related by a mapping that takes coordinate values in the old system and returns coordinate values in the new system.
| CoordinateTransformData[transf,"Mapping"] | the mapping between coordinate systems as a pure function |
| CoordinateTransformData[transf,"Mapping",pt] | the new coordinate values of pt |
| CoordinateTransform[transf,pt] | the new coordinate values of pt |
The function CoordinateTransformData returns information about mappings between the coordinate systems in CoordinateChartData.
This converts the point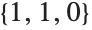 
in Cartesian coordinates to the corresponding 
values in spherical coordinates:
in Cartesian coordinates to the corresponding 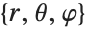values in spherical coordinates:The mapping function can be requested from CoordinateTransformData and stored for later use:
Using Map, it can be applied to several points at once:
The function CoordinateTransform provides a convenient mechanism for converting one or several points.
Parameters can be specified in CoordinateTransform in the same way as in CoordinateTransformData. This converts a generic point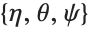 
from prolate spheroidal coordinates with parameter 
to hyperspherical coordinates:
from prolate spheroidal coordinates with parameter 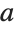to hyperspherical coordinates:When transforming fields between two coordinate systems, a field given in terms of variables in the old system is re-expressed in terms of variables in the new system. In addition to the mapping between the systems, several additional steps are needed: solving for the old variables in terms of the new, substituting in these expressions, and, in the case of vector and tensor fields, accounting for differences in basis vectors between the two coordinate systems. All of these steps are performed by the command TransformedField.
| TransformedField[transf,f,{x1,x2,…,xn}->{y1,y2,…,yn}] | transform a scalar, vector, or tensor field f from coordinates xi to coordinates yi |
The previous example can be done "by hand". Unlike for CoordinateTransform, for these steps to make sense,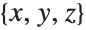 
and 
must be coordinate names and not coordinate values such as numbers:
and 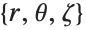must be coordinate names and not coordinate values such as numbers:Parameters can be specified in TransformedField in the same way as in CoordinateTransformData. This is a transformation from cylindrical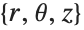 
to prolate spheroidal 
coordinates with parameter 
:
to prolate spheroidal coordinates with parameter 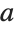:The vector and tensor case is more complicated because of the need to account for the change of basis vectors. As a result, the transformation of a vector is not merely the transformation of its components. For arrays, which are interpreted as components in an orthonormal basis, the rotation matrix that relates the two bases is given by the CoordinateTransformData property "OrthonormalBasisRotation".
This converts the vector field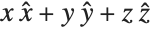 
from Cartesian 
coordinates to spherical 
coordinates, producing the manifestly radial result 
:
from Cartesian 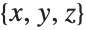coordinates to spherical 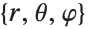coordinates, producing the manifestly radial result 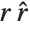:Two pieces of information are needed to reproduce the previous example: the variable replacement rules, as in the scalar case, and the basis rotation matrix. Since the rotation matrix specifies the rotation between bases, its transpose is the matrix that acts on components:
To transform a vector between coordinate systems, first the vector is multiplied by the rotation matrix to change components in the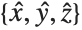 
basis to components in the 
basis (equivalently, the projection of the vector onto the local basis vectors). Subsequently, the replacement rules are applied:
basis to components in the 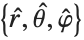basis (equivalently, the projection of the vector onto the local basis vectors). Subsequently, the replacement rules are applied:Using Map, lists of scalar fields can be transformed between coordinates. The result is quite different from transforming a vector field with the same components:
The vector field in hyperspherical coordinates with the same local components is in fact a rotational vector field about the 
axis:
axis:Parameters for coordinate systems can be specified in TransformedField. This converts the vector field 
from Cartesian 
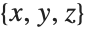coordinates to prolate spheroidal 
coordinates with parameter 
:
from Cartesian coordinates to prolate spheroidal coordinates with parameter 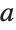:Using Map, it is possible to transform the matrix as a list of two vectors or as a matrix of four scalar fields. The results are quite different in each case:
The basis rotation matrix used above combines information about both the Jacobian matrix of the mapping and the orthonormal basis in each chart. For orthogonal coordinate systems, it is constructed from the Jacobian and the two sets of scale factors.
| CoordinateTransformData[transf,prop,pt] | compute a property of the transformation at the point pt |
| CoordinateChartData[chart,prop,pt] | compute a property of the chart at the point pt |
To compute the rotation matrix, the scale factors, which define the orthonormal bases in orthogonal systems, are needed. Notice that CoordinateTransform is used to ensure both sets of scale factors are evaluated at the same point:
