Vector Analysis
Vector analysis forms the basis of many physical and mathematical models. The Wolfram Language can compute the basic operations of gradient, divergence, curl, and Laplacian in a variety of coordinate systems. Moreover, these operators are implemented in a quite general form, allowing them to be used in different dimensions and with higher-rank tensors.
Vector Derivatives
| Grad[f,{x1,…,xn}] | gradient of a scalar function |
| Div[{f1,…,fn},{x1,…,xn}] | divergence of a vector-valued function |
| Curl[{f1,…,fn},{x1,…,xn}] | curl of a vector-valued function |
| Laplacian[f,{x1,…,xn}] | Laplacian of a scalar function |
Although these operators are available in any dimension, they are most commonly encountered in three dimensions.
The curl is not restricted to three dimensions. This gives a two-dimensional curl, which is a scalar:
The meaning of the curl in dimensions other than three is discussed more fully in the next subsection.
Generalization to Higher-Rank Tensors
All four operators introduced in the previous subsection are general operators that can take vectors and higher-rank tensors as input. For Curl in dimension 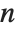 , the input can be a scalar, vector, or tensor of rank up to
, the input can be a scalar, vector, or tensor of rank up to  . For the other functions, the allowed rank of input tensors is unlimited.
. For the other functions, the allowed rank of input tensors is unlimited.
The divergence is a gradient followed by contraction of the last two slots. It therefore reduces the rank by 1:
It is possible to take the divergence in a slot other than the final one by using TensorContract:
The reason for this behavior is that the curl is the Hodge dual of the anti-symmetrized gradient. This explains the restriction on rank:
Known Coordinate Charts
The Wolfram Language contains information about a large number of coordinate charts. The function CoordinateChartData provides a mechanism for retrieving this information.
| CoordinateChartData[{"coordsys",n}] | standard name for |
| CoordinateChartData[{All,n}] | available coordinate charts in |
| CoordinateChartData[{All,All,n}] | available coordinate charts in |
| CoordinateChartData[chart,"prop"] | property "prop" for the specified coordinate chart |
| CoordinateChartData[chart,"prop",pt] | property "prop" for the specified coordinate chart at the point pt |
The following examples show how to look up available coordinate charts. In their most general form, coordinate chart specifications contain a coordinate system name, a metric, and a dimension. Note that many charts require parameters. These can be specified or left at the shown defaults.
Although the coordinate chart standard names are quite long, it is typically possible to omit "Euclidean" and the dimension when using Euclidean coordinate charts.
CoordinateChartData contains many properties regarding the different coordinate charts. The most fundamental is the metric, which ultimately determines all lengths and volumes in the coordinate chart. However, in the context of vector analysis in orthogonal coordinates, it is more common to consider the scale factors and volume factor.
This gives the scale factors for elliptic coordinates along a curve 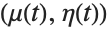 . Notice that the default parameter
. Notice that the default parameter 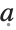 has been used:
has been used:
The physical speed is then the norm of the velocity. This could also have been obtained directly from the metric and coordinate velocity:
This gives the volume factor in bipolar coordinates with the parameter set to 1. Notice that a double list is needed to ensure that 1 is treated as a parameter instead of a dimension:
Vector Derivatives in Non-Cartesian Coordinates
The four vector derivative operators work in any coordinate chart. It is only necessary to specify the chart in the third argument of the function.
| Grad[f,{x1,…,xn},chart] | gradient in the specified coordinate chart |
| Div[{f1,…,fn},{x1,…,xn},chart] | divergence in the specified coordinate chart |
| Curl[{f1,…,fn},{x1,…,xn},chart] | curl in the specified coordinate chart |
| Laplacian[f,{x1,…,xn},chart] | Laplacian in the specified coordinate chart |
Arrays are treated in these commands as components in the orthonormal basis. This applies to both input and output. As a result, the physical dot product can be computed using Dot.
In an orthogonal coordinate system, the gradient of a scalar equals the partial derivatives divided by the scale factors:
The gradient of vectors and higher-rank tensors introduces connection terms to the result, meaning it is not simply the gradient of each component:
Since the divergence only applies to vectors and tensors, it always has connection terms. However, since arrays are treated as being in the orthonormal basis, the divergence is still a gradient followed by a contraction:
Because of the connection terms, the divergence of a rank-2 tensor is not simply the divergence of each row:
By definition, the Laplacian is the divergence of the gradient. As a result, the Laplacian has connection terms in non-Cartesian coordinates as well:
When acting on scalars, there are no connection terms, but the normalization from the scale factors does appear in the result:
Classical Definitions
As seen above, the gradient of a scalar in orthogonal coordinates involves the partial derivatives and the scale factors. There are similar definitions for the divergence of a vector, the Laplacian of a scalar, and the curl of a vector in terms of the scale factors and volume factor.
The gradient in an orthogonal chart is related to the gradient in Cartesian coordinates by the scale factors:
In an orthogonal coordinate system, the classical formula for the divergence of a vector relates it to the divergence in Cartesian coordinates using the scale factors and volume factor:
Combining the classical formula for divergence with the definition of the gradient of a scalar in an orthogonal system produces a classical formula for the Laplacian:
The following illustrates a similar formula for the three-dimensional curl of a vector. To generalize to dimension 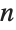 , replace the leading scales with the TensorProduct of
, replace the leading scales with the TensorProduct of  copies of scales:
copies of scales: