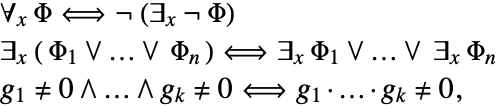Complex Polynomial Systems
| Introduction | Arbitrary Complex Polynomial Systems |
| Gröbner Bases | Options |
| Decision Problems | References |
| Quantifier Elimination |
Introduction
The Wolfram Language functions Reduce, Resolve, and FindInstance allow you to solve a wide variety of problems that can be expressed in terms of equations and inequalities. The functions use a collection of algorithms applicable to classes of problems satisfying particular properties, as well as a set of heuristics that attempt to reduce the given problem to a sequence of problems that can be solved using the algorithms. This tutorial describes the algorithms used to solve the class of problems known as complex polynomial systems. It characterizes the structure of the returned answers and describes the options that affect various aspects of the methods involved.
A complex polynomial system is an expression constructed with polynomial equations and inequations
combined using logical connectives and quantifiers
An occurrence of a variable ![]() inside
inside ![]() or
or ![]() is called a bound occurrence, and any other occurrence of
is called a bound occurrence, and any other occurrence of ![]() is called a free occurrence. A variable
is called a free occurrence. A variable ![]() is called a free variable of a complex polynomial system if the system contains a free occurrence of
is called a free variable of a complex polynomial system if the system contains a free occurrence of ![]() . A complex polynomial system is quantifier-free if it contains no quantifiers.
. A complex polynomial system is quantifier-free if it contains no quantifiers.
Here is an example of a complex polynomial system with free variables ![]() ,
, ![]() , and
, and ![]() .
.
In the Wolfram Language, quantifiers are represented using the functions Exists (![]() ) and ForAll (
) and ForAll (![]() ).
).
Any complex polynomial system can be transformed to the prenex normal form
where each ![]() is a quantifier
is a quantifier ![]() or
or ![]() , and
, and ![]() is quantifier-free.
is quantifier-free.
Any quantifier-free complex polynomial system can be transformed to the disjunctive normal form
where each ![]() is a polynomial equation or inequation.
is a polynomial equation or inequation.
Reduce, Resolve, and FindInstance always put complex polynomial systems in the prenex normal form, with quantifier-free parts in the disjunctive normal form, and subtract the sides of the equations and inequations to put them in the form
In all the tutorials for complex polynomial system solving, assume that the system has been transformed to this form.
Reduce can solve arbitrary complex polynomial systems. The solution (possibly after expanding ![]() with respect to
with respect to ![]() ) is a disjunction of terms of the form
) is a disjunction of terms of the form
where ![]() are the free variables of the system, each
are the free variables of the system, each ![]() is a polynomial, each
is a polynomial, each ![]() is an algebraic function expressed using radicals or Root objects, and any terms of the conjunction (2) may be absent. Each
is an algebraic function expressed using radicals or Root objects, and any terms of the conjunction (2) may be absent. Each ![]() is well defined, that is, no denominators or leading terms of Root objects in
is well defined, that is, no denominators or leading terms of Root objects in ![]() become zero for any
become zero for any ![]() satisfying the preceding terms of the conjunction (2).
satisfying the preceding terms of the conjunction (2).
Resolve can eliminate quantifiers from arbitrary complex polynomial systems. If no variables are specified, the result is a logical combination of terms
where ![]() and
and ![]() are polynomials, and each
are polynomials, and each ![]() is a free variable of the system. With variables specified in the input, Resolve gives the same answer as Reduce.
is a free variable of the system. With variables specified in the input, Resolve gives the same answer as Reduce.
FindInstance can handle arbitrary complex polynomial systems giving instances of complex solutions, or an empty list for systems that have no solutions. If the number of instances requested is more than one, the instances are randomly generated from the full solution of the system, and therefore they may depend on the value of the RandomSeed option. If one instance is requested, a faster algorithm that produces one instance is used, and the instance returned is always the same.
The main tool used in solving complex polynomial systems is the Gröbner basis algorithm [1], which is available in the Wolfram Language as the GroebnerBasis function.
Gröbner Bases
Theory
This section gives a very brief introduction to the theory of Gröbner bases. It presents only the properties that are necessary to describe the algorithms used by the Wolfram Language in solving complex polynomial systems. For a more complete presentation see, for example, [1, 2]. Note that what [2] calls a monomial, [1] calls a term, and vice versa. This tutorial uses the terminology of [1].
A monomial in ![]() is an expression of the form
is an expression of the form ![]() with non‐negative integers
with non‐negative integers ![]() .
.
Let ![]() be the set of all monomials in
be the set of all monomials in ![]() . A monomial order is a linear order
. A monomial order is a linear order ![]() on
on ![]() , such that
, such that ![]() for all
for all ![]() , and
, and ![]() implies
implies ![]() for all
for all ![]() .
.
Let ![]() be a field, the domain of integers, or the domain of univariate polynomials over a field. Let
be a field, the domain of integers, or the domain of univariate polynomials over a field. Let ![]() and
and ![]() be functions
be functions ![]() defined as follows. If
defined as follows. If ![]() is a field,
is a field, ![]() , and
, and ![]() . If
. If ![]() is the domain of integers,
is the domain of integers, ![]() and
and ![]() are the integer quotient and remainder functions, with
are the integer quotient and remainder functions, with ![]() . If
. If ![]() is the domain of univariate polynomials over a field,
is the domain of univariate polynomials over a field, ![]() and
and ![]() are the polynomial quotient and remainder functions.
are the polynomial quotient and remainder functions.
A product ![]() , where
, where ![]() is a nonzero element of
is a nonzero element of ![]() and
and ![]() is a monomial, is called a term.
is a monomial, is called a term.
Let ![]() be a monomial order on
be a monomial order on ![]() , and let
, and let ![]() . The leading monomial
. The leading monomial ![]() of
of ![]() is the
is the ![]() -largest monomial appearing in
-largest monomial appearing in ![]() , the leading coefficient
, the leading coefficient ![]() of
of ![]() is the coefficient at
is the coefficient at ![]() in
in ![]() , and the leading term
, and the leading term ![]() of
of ![]() is the product
is the product ![]() .
.
A Gröbner basis of an ideal ![]() in
in ![]() , with respect to a monomial order
, with respect to a monomial order ![]() , is a finite set
, is a finite set ![]() of polynomials, such that for each
of polynomials, such that for each ![]() , there exists
, there exists ![]() , such that
, such that ![]() divides
divides ![]() . Every ideal
. Every ideal ![]() has a Gröbner basis (see [1] for a proof).
has a Gröbner basis (see [1] for a proof).
Let ![]() , and let
, and let ![]() be a monomial. A term
be a monomial. A term ![]() is reducible modulo
is reducible modulo ![]() , if
, if ![]() divides
divides ![]() , and
, and ![]() . If
. If ![]() is reducible modulo
is reducible modulo ![]() , the reduction of
, the reduction of ![]() modulo
modulo ![]() is the polynomial
is the polynomial
Note that if ![]() , then
, then ![]() ; otherwise,
; otherwise, ![]() .
.
Let ![]() , and let
, and let ![]() be an ordered finite subset of
be an ordered finite subset of ![]() .
. ![]() is reducible modulo
is reducible modulo ![]() if
if ![]() contains a term reducible modulo an element of
contains a term reducible modulo an element of ![]() . The reduction
. The reduction ![]() of
of ![]() modulo
modulo ![]() is defined by the following procedure. While the set
is defined by the following procedure. While the set ![]() of terms of
of terms of ![]() reducible modulo an element of
reducible modulo an element of ![]() is not empty, take the term
is not empty, take the term ![]() with the
with the ![]() -largest monomial, take the first
-largest monomial, take the first ![]() , such that
, such that ![]() is reducible modulo
is reducible modulo ![]() , and replace the term
, and replace the term ![]() in
in ![]() with
with ![]() . Note that the monomials of terms
. Note that the monomials of terms ![]() chosen in subsequent steps of the procedure form a
chosen in subsequent steps of the procedure form a ![]() -descending chain, and each monomial can appear at most
-descending chain, and each monomial can appear at most ![]() times, where
times, where ![]() is the number of elements of
is the number of elements of ![]() , hence the procedure terminates.
, hence the procedure terminates.
A Gröbner basis ![]() is semi-reduced if for all
is semi-reduced if for all ![]() ,
, ![]() is not reducible modulo
is not reducible modulo ![]() , and if
, and if ![]() is the domain of integers,
is the domain of integers, ![]() .
.
The Wolfram Language function GroebnerBasis returns semi-reduced Gröbner bases. In the following discussion, all Gröbner bases are assumed to be semi-reduced. Note that this is not the same as reduced Gröbner bases defined in the literature, since here the basis polynomials are not required to be monic. For a fixed monomial order, every ideal has a unique reduced Gröbner basis. Semi-reduced Gröbner bases defined here are only unique up to multiplication by invertible elements of ![]() (see Property 2).
(see Property 2).
Property 1: Let ![]() be a Gröbner basis of an ideal
be a Gröbner basis of an ideal ![]() in
in ![]() , and let
, and let ![]() . Then
. Then ![]() iff
iff ![]() .
.
This is a simple consequence of the definitions.
Property 2: Let ![]() and
and ![]() be two Gröbner bases of an ideal
be two Gröbner bases of an ideal ![]() with respect to the same monomial order
with respect to the same monomial order ![]() , and suppose that elements of
, and suppose that elements of ![]() and
and ![]() are ordered by their leading monomials. Then
are ordered by their leading monomials. Then ![]() , and for all
, and for all ![]() , if
, if ![]() is the domain of integers,
is the domain of integers, ![]() ; otherwise,
; otherwise, ![]() for some invertible element
for some invertible element ![]() of
of ![]() .
.
Proof: If ![]() , then
, then ![]() is reducible modulo
is reducible modulo ![]() or
or ![]() is reducible modulo
is reducible modulo ![]() . Hence the leading monomials of the elements of a Gröbner basis are all different. Without loss of generality, assume
. Hence the leading monomials of the elements of a Gröbner basis are all different. Without loss of generality, assume ![]() . For induction, fix
. For induction, fix ![]() and suppose that for all
and suppose that for all ![]() ,
, ![]() for some invertible element
for some invertible element ![]() of
of ![]() . If
. If ![]() is the domain of integers,
is the domain of integers, ![]() . Without loss of generality, assume
. Without loss of generality, assume ![]() . Since
. Since ![]() belongs to
belongs to ![]() , there exists
, there exists ![]() such that
such that ![]() divides
divides ![]() . Then
. Then ![]() , and so
, and so ![]() . If
. If ![]() , then
, then ![]() would be reducible modulo
would be reducible modulo ![]() and also modulo
and also modulo ![]() , which is impossible, since
, which is impossible, since ![]() is semi-reduced. Hence
is semi-reduced. Hence ![]() , and
, and ![]() , and
, and ![]() divides
divides ![]() . Similarly,
. Similarly, ![]() divides
divides ![]() . Therefore, there exists an invertible element
. Therefore, there exists an invertible element ![]() of
of ![]() , such that
, such that ![]() . If
. If ![]() is the domain of integers,
is the domain of integers, ![]() and
and ![]() are positive, and so
are positive, and so ![]() . Let
. Let ![]() . Suppose
. Suppose ![]() . Since
. Since ![]() belongs to
belongs to ![]() ,
, ![]() must be divisible by
must be divisible by ![]() , for some
, for some ![]() . Let
. Let ![]() and
and ![]() be the coefficients at
be the coefficients at ![]() in
in ![]() and
and ![]() . If
. If ![]() is a field, the term
is a field, the term ![]() of
of ![]() is reducible modulo
is reducible modulo ![]() , which contradicts the assumption that
, which contradicts the assumption that ![]() is semi-reduced. If
is semi-reduced. If ![]() is the domain of univariate polynomials over a field,
is the domain of univariate polynomials over a field,
and so either ![]() is reducible modulo
is reducible modulo ![]() , or
, or ![]() is reducible modulo
is reducible modulo ![]() , which contradicts the assumption that
, which contradicts the assumption that ![]() and
and ![]() are semi-reduced. Finally, let
are semi-reduced. Finally, let ![]() be the domain of integers. Since neither
be the domain of integers. Since neither ![]() is reducible modulo
is reducible modulo ![]() nor
nor ![]() is reducible modulo
is reducible modulo ![]() ,
, ![]() and
and ![]() . Hence
. Hence ![]() , which is impossible, since
, which is impossible, since ![]() is divisible by
is divisible by ![]() . Therefore
. Therefore ![]() , and so
, and so ![]() . By induction on
. By induction on ![]() , for all
, for all ![]() ,
, ![]() . If
. If ![]() , then
, then ![]() would be reducible modulo some
would be reducible modulo some ![]() , with
, with ![]() , and hence
, and hence ![]() would be reducible modulo
would be reducible modulo ![]() . Therefore
. Therefore ![]() , which completes the proof of Property 2.
, which completes the proof of Property 2.
Property 3: Let ![]() be an ideal in
be an ideal in ![]() , let
, let ![]() , and let
, and let ![]() be a Gröbner basis of the ideal
be a Gröbner basis of the ideal ![]() in
in ![]() . Then
. Then ![]() belongs to the radical of
belongs to the radical of ![]() iff
iff ![]() for an invertible element
for an invertible element ![]() of
of ![]() .
.
If an ideal contains invertible elements of ![]() , GroebnerBasis always returns
, GroebnerBasis always returns ![]() .
.
belongs to the ideal ![]() for any non‐negative integer
for any non‐negative integer ![]() . Hence, if
. Hence, if ![]() belongs to the radical of
belongs to the radical of ![]() , then 1 belongs to
, then 1 belongs to ![]() . Since
. Since ![]() is a Gröbner basis of
is a Gröbner basis of ![]() , it must contain an element
, it must contain an element ![]() whose leading coefficient divides 1. Hence
whose leading coefficient divides 1. Hence ![]() is an invertible element of
is an invertible element of ![]() . Since
. Since ![]() is semi-reduced and
is semi-reduced and ![]() divides any term,
divides any term, ![]() . Now suppose that
. Now suppose that ![]() for an invertible element
for an invertible element ![]() of
of ![]() . Then 1 belongs to
. Then 1 belongs to ![]() , and so
, and so
where each ![]() belongs to
belongs to ![]() , and each
, and each ![]() belongs to
belongs to ![]() . Hence comparing coefficients at powers of
. Hence comparing coefficients at powers of ![]() leads to the following equations modulo
leads to the following equations modulo ![]() :
: ![]() ,
, ![]() , for
, for ![]() , and
, and ![]() . Then,
. Then, ![]() , for
, for ![]() , and
, and ![]() modulo
modulo ![]() . Therefore,
. Therefore, ![]() belongs to the radical of
belongs to the radical of ![]() , which completes the proof of Property 3.
, which completes the proof of Property 3.
The following more technical property is important for solving complex polynomial systems.
Property 4: Let ![]() be a Gröbner basis of an ideal
be a Gröbner basis of an ideal ![]() in
in ![]() with a monomial order that makes monomials containing
with a monomial order that makes monomials containing ![]() greater than monomials not containing
greater than monomials not containing ![]() , let
, let ![]() be the element of
be the element of ![]() with the lowest positive degree
with the lowest positive degree ![]() in
in ![]() , let
, let ![]() be the leading coefficient of
be the leading coefficient of ![]() in
in ![]() , and let
, and let ![]() be all elements of
be all elements of ![]() that do not depend on
that do not depend on ![]() . Then for any polynomial
. Then for any polynomial ![]() and any point
and any point ![]() if
if ![]() ,
, ![]() , for
, for ![]() , and
, and ![]() , then
, then ![]() .
.
Proof: Consider the pseudoremainder ![]() of the division of
of the division of ![]() by
by ![]() as polynomials in
as polynomials in ![]() .
.
Since ![]() and
and ![]() belong to
belong to ![]() , so does
, so does ![]() . By Property 1, reduction of
. By Property 1, reduction of ![]() by
by ![]() must yield zero. Since the degree of
must yield zero. Since the degree of ![]() in
in ![]() is less than
is less than ![]() ,
, ![]() cannot be reduced by any of the elements of
cannot be reduced by any of the elements of ![]() that depend on
that depend on ![]() . Hence
. Hence
and so ![]() . Since
. Since ![]() , (1) implies that
, (1) implies that ![]() , which completes the proof of Property 4.
, which completes the proof of Property 4.
Wolfram Language Function GroebnerBasis
The Wolfram Language function GroebnerBasis finds semi-reduced Gröbner bases. This section describes GroebnerBasis options used in the solving of complex polynomial systems.
option name | default value | |
| CoefficientDomain | Automatic | the type of objects assumed to be coefficients |
| Method | Automatic | the method used to compute the basis |
| MonomialOrder | Lexicographic | the criterion used for ordering monomials |
GroebnerBasis options used in the solving of complex polynomial systems.
This option specifies the domain ![]() of coefficients. With the default Automatic setting, the coefficient domain is the field generated by numeric coefficients present in the input.
of coefficients. With the default Automatic setting, the coefficient domain is the field generated by numeric coefficients present in the input.
| Integers | the domain of integers |
| InexactNumbers[prec] | inexact numbers with precision prec |
| Polynomials[x] | the domain of polynomials in |
| RationalFunctions | the field of rational functions in variables not on the variable list given to GroebnerBasis |
| Rationals | the field of rational numbers |
Available settings for CoefficientDomain.
Note that the coefficient domain ![]() also depends on the setting of the Modulus option of GroebnerBasis. With Modulus->p, for a prime number
also depends on the setting of the Modulus option of GroebnerBasis. With Modulus->p, for a prime number ![]() , the coefficient domain is the field
, the coefficient domain is the field ![]() , or the field of rational functions over
, or the field of rational functions over ![]() if CoefficientDomain->RationalFunctions.
if CoefficientDomain->RationalFunctions.
With the default setting Method->Automatic, GroebnerBasis normally uses a variant of the Buchberger algorithm. Another algorithm available is the Gröbner walk, which computes a Gröbner basis in an easier monomial order and then transforms it to the required harder monomial order. This is often faster than directly computing a Gröbner basis in the required order, especially if the input polynomials are known to be a Gröbner basis for the easier order. With the Method->Automatic setting, GroebnerBasis uses the Gröbner walk for the default CoefficientDomain->Rationals and MonomialOrder->Lexicographic.
| GroebnerBasis[polys,vars,Method->{"GroebnerWalk","InitialMonomialOrder"->order1},MonomialOrder->order2] | |
| find a Gröbner basis in order1 and use the Gröbner walk algorithm to transform it to a Gröbner basis in order2 | |
Transforming Gröbner bases using the Gröbner walk algorithm.
This option specifies the monomial order. The value can be either one of the named monomial orders or a weight matrix. The following table gives conditions for ![]() .
.
Quantifier elimination needs an order in which monomials containing quantifier variables are greater than monomials not containing quantifier variables. The Lexicographic order satisfies this condition, but the following EliminationOrder usually leads to faster computations.
where ![]() denotes total degree,
denotes total degree, ![]() denotes free variables,
denotes free variables, ![]() denotes quantifier variables,
denotes quantifier variables, ![]() and
and ![]() are monomials, and
are monomials, and ![]() denotes the DegreeReverseLexicographic order.
denotes the DegreeReverseLexicographic order.
Using EliminationOrder requires the GroebnerBasis syntax with elimination variables specified.
| GroebnerBasis[polys,xvars,yvars,MonomialOrder->EliminationOrder] | |
| find a Gröbner basis in EliminationOrder | |
Gröbner basis in elimination order.
By default, GroebnerBasis with MonomialOrder->EliminationOrder drops the polynomials that contain ![]() from the result, returning only basis polynomials in
from the result, returning only basis polynomials in ![]() . To get all basis polynomials, the value of the system option EliminateFromGroebnerBasis from the GroebnerBasisOptions group must be changed. (The Wolfram Language changes the option locally in the quantifier elimination algorithm.) The option value can be changed with
. To get all basis polynomials, the value of the system option EliminateFromGroebnerBasis from the GroebnerBasisOptions group must be changed. (The Wolfram Language changes the option locally in the quantifier elimination algorithm.) The option value can be changed with
SetSystemOptions["GroebnerBasisOptions"->{"EliminateFromGroebnerBasis"->False}].
option name | default value | |
| "EliminateFromGroebnerBasis" | True | whether GroebnerBasis with MonomialOrder->EliminationOrder should remove polynomials containing elimination variables |
System option EliminateFromGroebnerBasis.
Decision Problems
A decision problem is a system with all variables existentially quantified, that is, a system of the form
where ![]() are all variables in
are all variables in ![]() . Solving a decision problem means deciding whether it is equivalent to True or to False, that is, deciding whether the quantifier-free system of polynomial equations and inequations
. Solving a decision problem means deciding whether it is equivalent to True or to False, that is, deciding whether the quantifier-free system of polynomial equations and inequations ![]() has solutions.
has solutions.
solving any decision problem can be reduced to solving a finite number of decision problems of the form
By Hilbert's Nullstellensatz and Property 3 of Gröbner bases
with an arbitrary monomial order, is different than {1}.
When the Wolfram Language solves a decision problem, the monomial order used by the GroebnerBasis computation is MonomialOrder->EliminationOrder, with {z} specified as the elimination variable list. This setting corresponds to the monomial ordering in which monomials containing z are greater than those that do not contain z, and the ordering of monomials not containing z is degree reverse lexicographic. If there is no inequation condition, there is no need to introduce z, and the Wolfram Language uses MonomialOrder->DegreeReverseLexicographic.
Quantifier Elimination
For any complex polynomial system there exists an equivalent quantifier-free complex polynomial system. This follows from Chevalley's theorem, which states that a projection of a quasi-algebraically constructible set (a solution set of a quantifier-free system of polynomial equations and inequations) is a quasi-algebraically constructible set [3]. Quantifier elimination is the procedure of finding a quantifier-free complex polynomial system equivalent to a given complex polynomial system. In the Wolfram Language, quantifier elimination for complex polynomial systems is done by Resolve. It is also used by Reduce and FindInstance as the first step in solving or finding instances of solutions of complex polynomial systems.
For complex polynomial systems the Wolfram Language uses the following quantifier elimination method. Given the identities
eliminating quantifiers from any complex polynomial system can be reduced to a finite number of single existential quantifier eliminations from systems of the form
To eliminate the quantifier from (1), the Wolfram Language first computes the Gröbner basis of equations
with a monomial order that makes monomials containing ![]() greater than monomials not containing
greater than monomials not containing ![]() .
.
The monomial order used is EliminationOrder, with ![]() specified as the elimination variable list and all basis polynomials kept.
specified as the elimination variable list and all basis polynomials kept.
If ![]() contains no polynomials that depend on
contains no polynomials that depend on ![]() , then a quantifier-free system equivalent to (1) can be obtained by equating all elements of
, then a quantifier-free system equivalent to (1) can be obtained by equating all elements of ![]() to zero, and asserting that at least one coefficient of
to zero, and asserting that at least one coefficient of ![]() as a polynomial in
as a polynomial in ![]() is not equal to zero. Otherwise let
is not equal to zero. Otherwise let ![]() be the element of
be the element of ![]() with the lowest positive degree
with the lowest positive degree ![]() in
in ![]() , let
, let ![]() be the leading coefficient of
be the leading coefficient of ![]() in
in ![]() , and let
, and let ![]() be all elements of
be all elements of ![]() that do not depend on
that do not depend on ![]() . Now (1) can be split into a disjunction of two systems
. Now (1) can be split into a disjunction of two systems
To eliminate the quantifier from (2), the quantifier elimination procedure is called recursively. Since the ideal generated by ![]() strictly contains the ideal generated by
strictly contains the ideal generated by ![]() , the Noetherian property of polynomial rings guarantees finiteness of the recursion.
, the Noetherian property of polynomial rings guarantees finiteness of the recursion.
If ![]() belongs to the radical of the ideal generated by
belongs to the radical of the ideal generated by ![]() , which is exactly when 1 belongs to
, which is exactly when 1 belongs to
(3) is equivalent to False. Otherwise let
be the pseudoremainder of the division of ![]() by
by ![]() as polynomials in
as polynomials in ![]() . Then (3) is equivalent to the quantifier-free system
. Then (3) is equivalent to the quantifier-free system
To show that (3) implies (4), suppose that ![]() satisfies (3). Then
satisfies (3). Then ![]() and there exists
and there exists ![]() , such that
, such that
Since ![]() and
and ![]() belong to the ideal generated by
belong to the ideal generated by ![]() ,
,
To show that (4) implies (3), suppose that ![]() satisfies (4). Then
satisfies (4). Then
Since ![]() is a polynomial of degree
is a polynomial of degree ![]() , and
, and ![]() is a nonzero polynomial of degree less than
is a nonzero polynomial of degree less than ![]() , there is a root
, there is a root ![]() of
of ![]() such that
such that ![]() divides
divides ![]() but not
but not ![]() for some
for some ![]() . If
. If ![]() were zero, then
were zero, then ![]() would divide
would divide ![]() , which is impossible because it would imply that
, which is impossible because it would imply that ![]() divides
divides ![]() . Therefore
. Therefore ![]() . Property 4 shows that
. Property 4 shows that ![]() for any polynomial
for any polynomial ![]() . Since
. Since ![]() is a Gröbner basis of the ideal generated by
is a Gröbner basis of the ideal generated by ![]() ,
,
which completes the proof of correctness of the quantifier elimination algorithm.
Arbitrary Complex Polynomial Systems
FindInstance
FindInstance can handle arbitrary complex polynomial systems giving instances of complex solutions, or an empty list for systems that have no solutions. If the number of instances requested is more than one, the instances are randomly generated from the full solution of the system given by Reduce. If one instance is requested, a faster algorithm that produces one instance is used. Here is a description of the algorithm used to find a single instance, or prove that a system has no solutions.
If the system contains general quantifiers (![]() ), the quantifier elimination algorithm is used to eliminate the innermost quantifiers until the system contains only existential quantifiers (
), the quantifier elimination algorithm is used to eliminate the innermost quantifiers until the system contains only existential quantifiers (![]() ) or is quantifier-free. Note that
) or is quantifier-free. Note that
has solutions if and only if ![]() has solutions, and if
has solutions, and if ![]() is a solution of
is a solution of ![]() , then
, then ![]() is a solution of (1). Hence to find instances of solutions of systems containing only existential quantifiers it is enough to be able to find instances of quantifier-free systems. Moreover,
is a solution of (1). Hence to find instances of solutions of systems containing only existential quantifiers it is enough to be able to find instances of quantifier-free systems. Moreover, ![]() is a solution of
is a solution of
if and only if it is a solution of one of the ![]() , with
, with ![]() , so it is enough to show how to find instances of solutions of
, so it is enough to show how to find instances of solutions of
First compute the GroebnerBasis ![]() of
of ![]() with MonomialOrder->EliminationOrder, eliminating the polynomials that depend on
with MonomialOrder->EliminationOrder, eliminating the polynomials that depend on ![]() (if there is no inequation condition,
(if there is no inequation condition, ![]() is the GroebnerBasis of
is the GroebnerBasis of ![]() with MonomialOrder->DegreeReverseLexicographic). If
with MonomialOrder->DegreeReverseLexicographic). If ![]() contains 1, there are no solutions. Otherwise, compute a subset
contains 1, there are no solutions. Otherwise, compute a subset ![]() of
of ![]() of the highest cardinality among subsets strongly independent modulo the ideal generated by
of the highest cardinality among subsets strongly independent modulo the ideal generated by ![]() with respect to the degree reverse lexicographic order ([1], Section 9.3). Reorder
with respect to the degree reverse lexicographic order ([1], Section 9.3). Reorder ![]() so that
so that ![]() , and compute the lexicographic order GroebnerBasis
, and compute the lexicographic order GroebnerBasis ![]() of the ideal generated by
of the ideal generated by ![]() . To compute
. To compute ![]() , the Wolfram Language uses the Gröbner walk algorithm.
, the Wolfram Language uses the Gröbner walk algorithm.
For each of the variables ![]() ,
, ![]() , select the polynomial
, select the polynomial ![]() with the smallest leading monomial among elements of
with the smallest leading monomial among elements of ![]() that depend on
that depend on ![]() and not on
and not on ![]() . Let
. Let ![]() be the leading coefficient of
be the leading coefficient of ![]() as a polynomial in
as a polynomial in ![]() . If
. If ![]() depends on a variable that is not in
depends on a variable that is not in ![]() , replace
, replace ![]() with the lexicographic order Gröbner basis of the ideal generated by
with the lexicographic order Gröbner basis of the ideal generated by ![]() and
and ![]() . The following shows that this operation keeps
. The following shows that this operation keeps ![]() strongly independent modulo the ideal generated by
strongly independent modulo the ideal generated by ![]() . Hence, possibly after a finite (by the Noetherian property of polynomial rings) number of extensions of
. Hence, possibly after a finite (by the Noetherian property of polynomial rings) number of extensions of ![]() , the leading coefficient
, the leading coefficient ![]() of
of ![]() depends only on
depends only on ![]() , for all
, for all ![]() . For the set of polynomials
. For the set of polynomials ![]() , let
, let ![]() be the set of common zeros of elements of
be the set of common zeros of elements of ![]() . Both
. Both ![]() and
and ![]() have dimension
have dimension ![]() , and
, and ![]() , hence any
, hence any ![]() -dimensional irreducible component of
-dimensional irreducible component of ![]() is also a component of
is also a component of ![]() . Since
. Since ![]() does not vanish on any irreducible component of
does not vanish on any irreducible component of ![]() , it does not vanish on any
, it does not vanish on any ![]() -dimensional irreducible component of
-dimensional irreducible component of ![]() . Therefore, the Gröbner basis of
. Therefore, the Gröbner basis of ![]() and
and ![]() contains a polynomial
contains a polynomial ![]() depending only on
depending only on ![]() . Let
. Let ![]() . To find a solution of (2), pick its last
. To find a solution of (2), pick its last ![]() coordinates
coordinates ![]() so that
so that ![]() . For all
. For all ![]() ,
, ![]() , and so by Property 4 if
, and so by Property 4 if ![]() , for
, for ![]() , is chosen to be the first root of
, is chosen to be the first root of ![]() , then
, then ![]() . Moreover,
. Moreover, ![]() , because otherwise
, because otherwise ![]() would belong to
would belong to ![]() , which would imply that
, which would imply that ![]() , which is impossible since
, which is impossible since ![]() divides
divides ![]() .
.
To prove the correctness of the aforementioned algorithm, it must be shown that extending ![]() by
by ![]() that depend on a variable not in
that depend on a variable not in ![]() preserves strong independence of
preserves strong independence of ![]() modulo the ideal generated by
modulo the ideal generated by ![]() . Suppose for some
. Suppose for some ![]() ,
, ![]() depends on a variable, which is not in
depends on a variable, which is not in ![]() . Let
. Let ![]() denote the ideal generated by
denote the ideal generated by ![]() , and let
, and let ![]() denote the ideal generated by
denote the ideal generated by ![]() and
and ![]() . Then
. Then ![]() does not contain nonzero elements of
does not contain nonzero elements of ![]() . To prove this, suppose that
. To prove this, suppose that ![]() where
where ![]() and
and ![]() . Then
. Then ![]() , with
, with ![]() , and
, and
belongs to the ideal generated by ![]() , and so does
, and so does ![]() . This contradicts the choice of
. This contradicts the choice of ![]() since the leading monomial of
since the leading monomial of ![]() depends on
depends on ![]() and is strictly smaller than the leading monomial of
and is strictly smaller than the leading monomial of ![]() . Therefore, the projection of
. Therefore, the projection of ![]() on
on ![]() is dense in
is dense in ![]() , and so, since
, and so, since ![]() has dimension
has dimension ![]() ,
, ![]() must be zero on some irreducible component
must be zero on some irreducible component ![]() of
of ![]() whose projection on
whose projection on ![]() is dense in
is dense in ![]() . Since
. Since ![]() is the Zariski closure of the projection of the
is the Zariski closure of the projection of the ![]() -dimensional set
-dimensional set ![]() ,
, ![]() is contained in the Zariski closure of the projection of an irreducible component
is contained in the Zariski closure of the projection of an irreducible component ![]() of
of ![]() .
. ![]() has dimension
has dimension ![]() , hence
, hence ![]() is zero on
is zero on ![]() , and the projection of
, and the projection of ![]() on
on ![]() is dense in
is dense in ![]() , which proves that
, which proves that ![]() is strongly independent modulo the ideal generated by
is strongly independent modulo the ideal generated by ![]() and
and ![]() .
.
Reduce
Reduce can solve arbitrary complex polynomial systems. As the first step, Reduce uses the quantifier elimination algorithm to eliminate the quantifiers. If the obtained quantifier-free system is a disjunction, each term of the disjunction is solved separately, and the solution is given as a disjunction of the solutions of the terms. Thus, the problem is reduced to solving quantifier-free systems of the form
First compute the GroebnerBasis ![]() of
of ![]() with variable order
with variable order ![]() and MonomialOrder->Lexicographic, and select the polynomials that do not depend on
and MonomialOrder->Lexicographic, and select the polynomials that do not depend on ![]() . Then the solution set of
. Then the solution set of ![]() is equal to the solution set of (3) and
is equal to the solution set of (3) and ![]() does not vanish on any component of the zero set
does not vanish on any component of the zero set ![]() of
of ![]() . If
. If ![]() contains 1, (3) has no solutions. Otherwise for each
contains 1, (3) has no solutions. Otherwise for each ![]() , such that the set
, such that the set ![]() of elements of
of elements of ![]() depending on
depending on ![]() and not on any
and not on any ![]() with
with ![]() is not empty, select an element
is not empty, select an element ![]() of
of ![]() with the lowest positive degree in
with the lowest positive degree in ![]() . If one of the leading coefficients
. If one of the leading coefficients ![]() of
of ![]() is zero on
is zero on ![]() , that is, it belongs to the radical of the ideal generated by
, that is, it belongs to the radical of the ideal generated by ![]() , replace
, replace ![]() by the lexicographic Gröbner basis of the ideal generated by
by the lexicographic Gröbner basis of the ideal generated by ![]() and
and ![]() . Now split the system into
. Now split the system into
and call the solving procedure recursively on all but the last term of the disjunction (4). Note that the algebraic set ![]() is strictly contained in
is strictly contained in ![]() , so the recursion is finite. If the product of all the
, so the recursion is finite. If the product of all the ![]() and
and ![]() belongs to the radical of the ideal generated by
belongs to the radical of the ideal generated by ![]() , the last term has no solutions. Otherwise, by Property 4, the solution set of the last term is equal to
, the last term has no solutions. Otherwise, by Property 4, the solution set of the last term is equal to
The conditions ![]() guarantee that all the solutions (represented as radicals or Root objects) given by Roots[hij0,xij] are well defined. Reduce performs several operations in order to simplify the inequation conditions returned, like removing multiple factors, removing factors common with earlier inequation conditions, reducing modulo the
guarantee that all the solutions (represented as radicals or Root objects) given by Roots[hij0,xij] are well defined. Reduce performs several operations in order to simplify the inequation conditions returned, like removing multiple factors, removing factors common with earlier inequation conditions, reducing modulo the ![]() , and removing factors that are nonzero on
, and removing factors that are nonzero on ![]() .
.
Options
Options for Reduce, Resolve, and FindInstance
The Wolfram Language functions for solving complex polynomial systems have a number of options that control the way they operate. This section gives a summary of these options.
option name | default value | |
| Backsubstitution | False | whether the solutions given by Reduce and Resolve with specified variables should be unwound by backsubstitution |
| Cubics | False | whether the Cardano formulas should be used to express solutions of cubics |
| Quartics | False | whether the Cardano formulas should be used to express solutions of quartics |
Options of Reduce and Resolve affecting the behavior of complex polynomial systems.
option name | default value | |
| WorkingPrecision | ∞ | the working precision to be used in computations, with the default settings of system options; the value of working precision affects only calls to Roots |
Options of Reduce, Resolve, and FindInstance affecting the behavior of complex polynomial systems.
The ReduceOptions Group of System Options
Here are the system options from the ReduceOptions group that may affect the behavior of Reduce, Resolve, and FindInstance for complex polynomial systems. The options can be set with
SetSystemOptions["ReduceOptions"->{"option name"->value}].
option name | default value | |
| "AlgebraicNumberOutput" | True | whether Reduce should output AlgebraicNumber objects instead of polynomials in one Root object |
| "FinitePrecisionGB" | False | whether finite values of working precision should be used in calls to GroebnerBasis |
| "ReorderVariables" | Automatic | whether Reduce, Resolve, and Solve are allowed to reorder the specified variables |
| "UseNestedRoots" | Automatic | whether Root objects representing algebraic numbers defined by triangular systems of equations can be used in the output |
ReduceOptions group options that affect the behavior of Reduce, Resolve, and FindInstance for complex polynomial systems.
For systems with equational constraints generating a zero-dimensional ideal ![]() , the Wolfram Language uses a variant of the CAD algorithm that finds projection polynomials using Gröbner basis methods. If the lexicographic order Gröbner basis of
, the Wolfram Language uses a variant of the CAD algorithm that finds projection polynomials using Gröbner basis methods. If the lexicographic order Gröbner basis of ![]() contains linear polynomials with constant coefficients in every variable but the last one (which is true "generically"), then all coordinates of a solution are polynomials in one algebraic number, namely the last coordinate. The setting of AlgebraicNumberOutput determines whether Reduce represents the solution coordinates as AlgebraicNumber objects in the field generated by the last coordinate.
contains linear polynomials with constant coefficients in every variable but the last one (which is true "generically"), then all coordinates of a solution are polynomials in one algebraic number, namely the last coordinate. The setting of AlgebraicNumberOutput determines whether Reduce represents the solution coordinates as AlgebraicNumber objects in the field generated by the last coordinate.