Input and Output in Notebooks

Entering Greek Letters	Other Mathematical Notation
Entering Two‐Dimensional Input	Mixing Text and Formulas
Editing and Evaluating Two‐Dimensional Expressions	Displaying and Printing Wolfram System Notebooks
Entering Formulas	Setting Up Hyperlinks
Entering Tables and Matrices	Automatic Numbering
Subscripts, Bars, and Other Modifiers	Exposition in Wolfram System Notebooks
Non‐English Characters and Keyboards	Named Characters

Entering Greek Letters

click on α	use a button in a palette
\[Alpha]	use a full name
EscaEsc or EscalphaEsc	use a standard alias (shown below as Esc a Esc )
Esc\alphaEsc	use a TeX alias
EscαEsc	use an HTML alias

Ways to enter Greek letters in a notebook.

Enter common Greek letters with a palette. Open it with the Palettes ▶ Special Characters menu item:

You can use Greek letters just like the ordinary letters that you type on your keyboard:

There are several ways to enter Greek letters. This input uses full names:

Commonly used Greek letters. TeX aliases are not listed explicitly.

Note that in the Wolfram Language the letter

stands for Pi. None of the other Greek letters have special meanings.

stands for Pi:

You can use Greek letters either on their own or with other letters:

The symbol

is not related to the symbol

Entering Two‐Dimensional Input

When the Wolfram Language reads the text x^y, it interprets it as x raised to the power y:

In a notebook, you can also give the two‐dimensional input x^y directly. The Wolfram Language again interprets this as a power:

One way to enter a two‐dimensional form such as x^y into a Wolfram System notebook is to paste this form into the notebook by clicking the appropriate button in the palette.

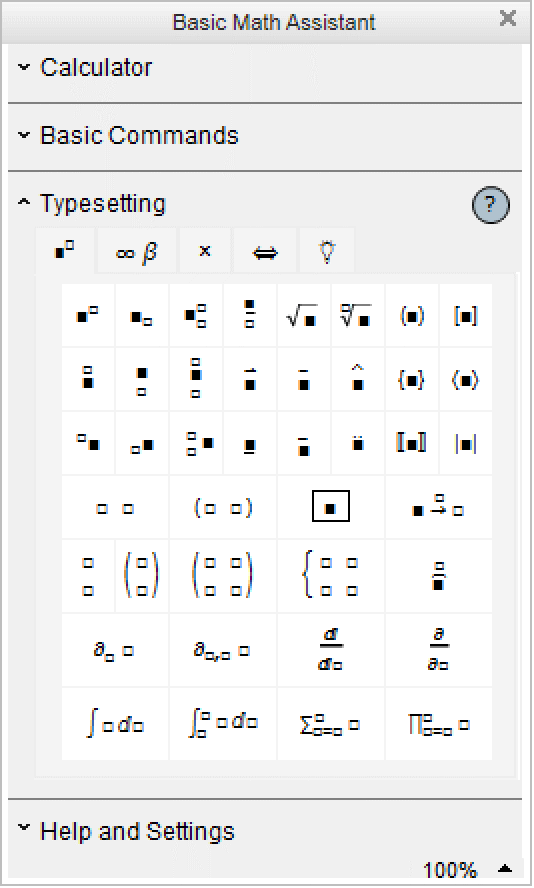
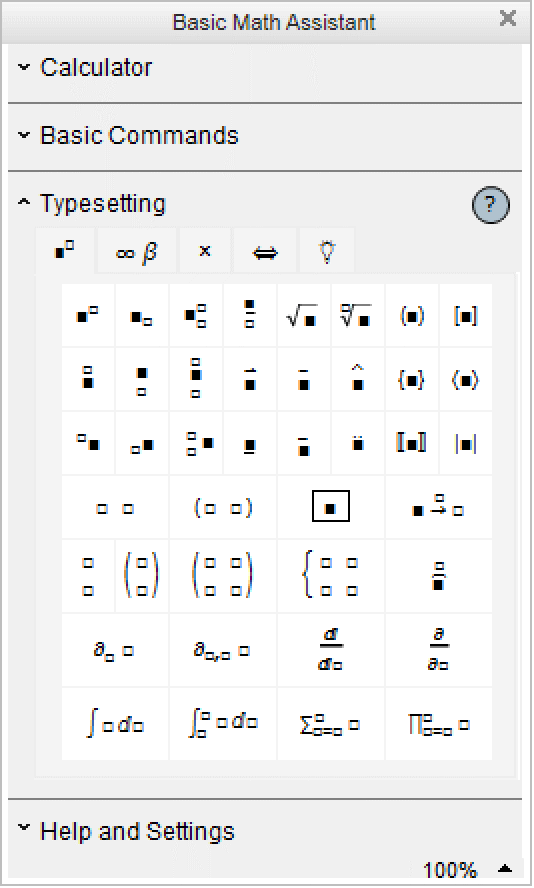
The Palettes ▶ Basic Math Assistant palette can be used to enter common two‐dimensional math notations.

There are also several ways to enter two‐dimensional forms directly from the keyboard.

x Ctrl+^ y Ctrl+Space	use control keys that exist on most keyboards
x Ctrl+6 y Ctrl+Space	use control keys that should exist on all keyboards

Ways to enter a superscript directly from the keyboard.

You type Ctrl+^ by holding down the Control key, then pressing the ^ key. As soon as you do this, your cursor will jump to a superscript position. You can then type anything you want and it will appear in that position.

When you have finished, press Ctrl+Space to move back down from the superscript position. You type Ctrl+Space by holding down the Control key, then pressing the Space bar.

This sequence of keystrokes enters x^y:

Here the whole expression y+z is in the superscript:

Pressing Ctrl+Space takes you down from the superscript:

You can remember the fact that Ctrl+^ gives you a superscript by thinking of Ctrl+^ as just a more immediate form of ^. When you type x^y, the Wolfram Language will leave this one‐dimensional form unchanged until you explicitly process it. But if you type x Ctrl+^ y then the Wolfram Language will immediately give you a superscript.

On a standard English‐language keyboard, the character ^ appears as the shifted version of 6. The Wolfram Language therefore accepts Ctrl+6 as an alternative to Ctrl+^. Note that if you are using something other than a standard English‐language keyboard, the Wolfram Language will almost always accept Ctrl+6 but may not accept Ctrl+^.

x Ctrl+_ y Ctrl+Space	use control keys that exist on most keyboards
x Ctrl+- y Ctrl+Space	use control keys that should exist on all keyboards

Ways to enter a subscript directly from the keyboard.

Subscripts in the Wolfram Language work very much like superscripts. However, whereas the Wolfram Language automatically interprets x^y as x raised to the power y, it has no similar interpretation for x_y. Instead, it just treats x_y as a purely symbolic object.

This enters y as a subscript:

Here is the usual one‐dimensional Wolfram Language input that gives the same output expression:

x Ctrl+/ y Ctrl+Space

use control keys

How to enter a built‐up fraction directly from the keyboard.

This enters the built‐up fraction

Here the whole y+z goes into the denominator:

But pressing Ctrl+Space takes you out of the denominator, so the +z does not appear in the denominator:

The Wolfram Language automatically interprets a built‐up fraction as a division:

Ctrl+@ x Ctrl+Space	use control keys that exist on most keyboards
Ctrl+2 x Ctrl+Space	use control keys that should exist on all keyboards

Ways to enter a square root directly from the keyboard.

This enters a square root:

Ctrl+Space takes you out of the square root:

Here is the usual one‐dimensional Wolfram Language input that gives the same output expression:

Ctrl+^ or Ctrl+6	go to the superscript position
Ctrl+_ or Ctrl+-	go to the subscript position
Ctrl+@ or Ctrl+2	go into a square root
Ctrl+% or Ctrl+5	go from subscript to superscript or vice versa, or to the exponent position in a root
Ctrl + /	go to the denominator for a fraction
Ctrl + Space	return from a special position

Special input forms based on control characters. The second forms given should work on any keyboard.

This puts both a subscript and a superscript on x:

Here is another way to enter the same expression:

The same procedure can be used to enter a definite integral:

In addition to subscripts and superscripts, the Wolfram Language also supports the notion of underscripts and overscripts—elements that go directly underneath or above. Among other things, you can use underscripts and overscripts to enter the limits of sums and products.

x Ctrl+Shift+, y Ctrl+Space
	create an underscript
x Ctrl+& y Ctrl+Space or x Ctrl+7 y Ctrl+Space
	create an overscript

Creating underscripts and overscripts.

Here is a way to enter a summation:

Editing and Evaluating Two‐Dimensional Expressions

When you see a two‐dimensional expression on the screen, you can edit it much as you would edit text. You can for example place your cursor somewhere and start typing. Or you can select a part of the expression, then remove it using the Delete key, or insert a new version by typing it in.

In addition to ordinary text editing features, there are some keys that you can use to move around in two‐dimensional expressions.

Ctrl + .	select the next larger subexpression
Ctrl + Space	move to the right of the current structure
→	move to the next character
←	move to the previous character

Ways to move around in two‐dimensional expressions.

This shows the sequence of subexpressions selected by repeatedly typing Ctrl+..

Shift + Enter	evaluate the whole current cell
Shift + Ctrl + Enter (Windows/Unix/Linux) or Cmd + Return (Mac OS X)
	evaluate only the selected subexpression

Ways to evaluate two‐dimensional expressions.

In most computations, you will want to go from one step to the next by taking the whole expression that you have generated, and then evaluating it. But if for example you are trying to manipulate a single formula to put it into a particular form, you may instead find it more convenient to perform a sequence of operations separately on different parts of the expression.

You do this by selecting each part you want to operate on, then inserting the operation you want to perform, then using Shift+Ctrl+Enter for Windows/Unix/Linux or Cmd+Return for Mac OS X.

Here is an expression with one part selected.

Pressing Shift+Ctrl+Enter (Windows/Unix/Linux) or Cmd+Return (Mac OS X) evaluates the selected part.

The Basic Commands ▶ y=x tab in the Basic Math Assistant, Classroom Assistant, and Writing Assistant palettes also provides a number of convenient operations which will transform in place any selected subexpression.

Entering Formulas

character	short form	long form	symbol
	EscpEsc	\[Pi]	Pi
	EscinfEsc	\[Infinity]	Infinity
	EscdegEsc	\[Degree]	Degree

Special forms for some common symbols.

This is equivalent to Sin[60Degree]:

Here is the long form of the input:

You can enter the same input like this:

Here the angle is in radians:

special characters	short form	long form	ordinary characters
x≤y	x Esc<=Esc y	x \[LessEqual] y	x <= y
x≥y	x Esc>=Esc y	x \[GreaterEqual] y	x >= y
x≠y	x Esc!=Esc y	x \[NotEqual] y	x != y
x∈y	x EscelEsc y	x \[Element] y	Element[x,y]
xy	x Esc->Esc y	x \[Rule] y	x -> y

Special forms for a few operators. "Operator Input Forms" gives a complete list.

Here the replacement rule is entered using two ordinary characters, as ->:

This means exactly the same:

As does this:

When you type the ordinary-character form for certain operators, the front end automatically replaces them with the special-character form. For instance, when you type the last three examples, the front end automatically substitutes the

character for ->.

The special arrow form

is by default also used for output:

special characters	short form	long form	ordinary characters
x ÷ y	x EscdivEsc y	x \[Divide] y	x / y
x × y	x Esc*Esc y	x \[Times] y	x * y
x  y	x EsccrossEsc y	x \[Cross] y	Cross[x,y]
x  y	x Esc==Esc y	x \[Equal] y	x == y
x  y	x Escl=Esc y	x \[LongEqual] y	x == y
x ∧ y	x Esc&&Esc y	x \[And] y	x && y
x ∨ y	x Esc\|\|Esc y	x \[Or] y	x \|\| y
¬ x	Esc!Esc x	\[Not] x	! x
x  y	x Esc=>Esc y	x \[Implies] y	x => y
x ⋃ y	x EscunEsc y	x \[Union] y	Union[x,y]
x ⋂ y	x EscinterEsc y	x \[Intersection] y	Intersection[x,y]
x y	x Esc,Esc y	x \[InvisibleComma] y	x , y
f x	f Esc@Esc x	f \[InvisibleApplication] x	f @ x or f[x]
x	x Esc+Esc	x \[ImplicitPlus]	x + y / z

Some operators with special forms used for input but not output.

The Wolfram Language understands

, but does not use it by default for output:

Many of the forms of input discussed here use special characters, but otherwise just consist of ordinary one‐dimensional lines of text. Wolfram System notebooks, however, also make it possible to use two‐dimensional forms of input.

two-dimensional	one-dimensional
	x^y	power
	x/y	division
	Sqrt[x]	square root
	x^(1/n)	^th root
	Sum[f,{i,i_min,i_max}]	sum
	Product[f,{i,i_min,i_max}]	product
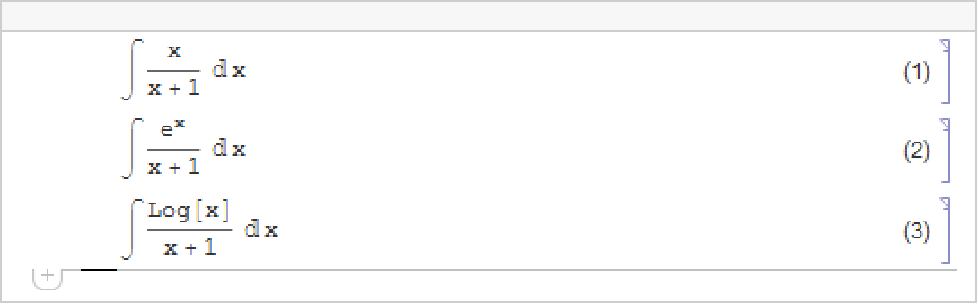
	Integrate[f,x]	indefinite integral
	Integrate[f,{x,x_min,x_max}]	definite integral
	D[f,x]	partial derivative
	D[f,x,y]	multivariate partial derivative
	Conjugate[x]	complex conjugate
	Transpose[m]	transpose
	ConjugateTranspose[m]	conjugate transpose
	Part[expr,i,j,…]	part extraction

Some two‐dimensional forms that can be used in Wolfram System notebooks.

You can enter two‐dimensional forms using any of the mechanisms discussed in "Entering Two-Dimensional Input". Note that upper and lower limits for sums and products must be entered as overscripts and underscripts—not superscripts and subscripts.

This enters an indefinite integral. Note the use of EscddEsc to enter the "differential d":

Here is an indefinite integral that can be explicitly evaluated:

Here is the usual Wolfram Language input for this integral:

short form	long form
EscsumEsc	\[Sum]	summation sign
EscprodEsc	\[Product]	product sign
EscintEsc	\[Integral]	integral sign
EscddEsc	\[DifferentialD]	special for use in integrals
EscpdEsc	\[PartialD]	partial derivative operator
EsccoEsc	\[Conjugate]	conjugate symbol
EsctrEsc	\[Transpose]	transpose symbol
EscctEsc	\[ConjugateTranspose]	conjugate transpose symbol
Esc[[Esc	\[LeftDoubleBracket]	part brackets

Some special characters used in entering formulas. "Mathematical and Other Notation" gives a complete list.

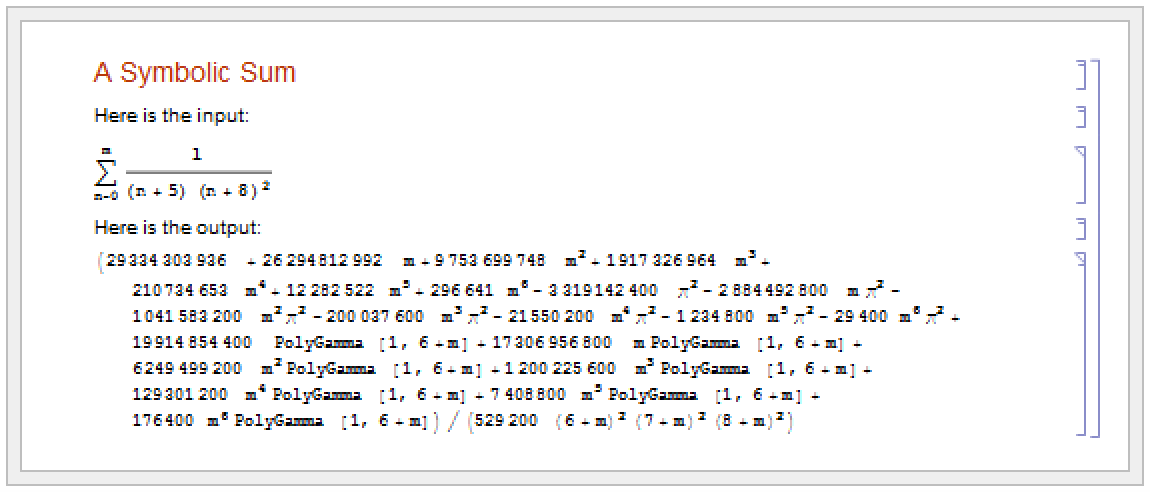
You should realize that even though a summation sign can look almost identical to a capital sigma it is treated in a very different way by the Wolfram Language. The point is that a sigma is just a letter; but a summation sign is an operator which tells the Wolfram Language to perform a Sum operation.

Capital sigma is just a letter:

A summation sign, on the other hand, is an operator:

Much as the Wolfram Language distinguishes between a summation sign and a capital sigma, it also distinguishes between an ordinary d, the "partial d" ∂ that is used for taking derivatives, and the special "differential d"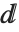

that is used in the standard notation for integrals. It is crucial that you use the differential

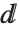—entered as EscddEsc—when you type in an integral. If you try to use an ordinary d, the Wolfram Language will just interpret this as a symbol called d—it will not understand that you are entering the second part of an integration operator.

This computes the derivative of

Here is the same derivative specified in ordinary one‐dimensional form:

This computes the third derivative:

Here is the equivalent one‐dimensional input form:

Entering Tables and Matrices

The Wolfram System front end provides an Insert ▶ Table/Matrix submenu for creating and editing arrays with any specified number of rows and columns. Once you have such an array, you can edit it to fill in whatever elements you want.

The Wolfram Language treats an array like this as a matrix represented by a list of lists:

Putting parentheses around the array makes it look more like a matrix, but does not affect its interpretation:

Using MatrixForm tells the Wolfram Language to display the result of the Transpose as a matrix:

Ctrl + ,	add a column
Ctrl + Enter	add a row
Tab	go to the next  or  element
Ctrl + Space	move out of the table or matrix

Entering tables and matrices.

Note that you can use Ctrl+, and Ctrl+Enter to start building up an array, and particularly for small arrays this is often more convenient than using the New menu item in the Table/Matrix submenu. The Table/Matrix menu items typically allow you to make basic adjustments, such as drawing lines between rows or columns.

Entering a Piecewise expression is a special case of entering a table.

Enter the \[Piecewise] character and press Ctrl+, to get a template of placeholders for two cases:

Fill in the placeholders to complete the piecewise expression:

To add additional cases, use Ctrl+Enter:

You can make an element in a table span over multiple rows or columns by selecting the entire block that you want the element to span and using the Insert ▶ Table/Matrix ▶ Make Spanning menu command. To split a spanning element into individual components, use Insert ▶ Table/Matrix ▶ Split Spanning.

To make the top element span across both columns, first select the row:

Now use the Make Spanning menu command.

Subscripts, Bars, and Other Modifiers

Here is a typical palette of modifiers.

The Wolfram Language allows you to use any expression as a subscript:

Unless you specifically tell it otherwise, the Wolfram System will interpret a superscript as a power:

Ctrl+_ or Ctrl+-	go to the position for a subscript
Ctrl + Shift + ,	go to the position underneath
Ctrl+^ or Ctrl+6	go to the position for a superscript
Ctrl+& or Ctrl+7	go to the position on top
Ctrl + Space	return from a special position

Special input forms based on control characters. The second forms given should work on any keyboard.

This enters a subscript using control keys:

Just as Ctrl+^ and Ctrl+_ go to superscript and subscript positions, so also Ctrl+& and Ctrl+4 can be used to go to positions directly above and below. With the layout of a standard English‐language keyboard Ctrl+& is directly to the right of Ctrl+^ while Ctrl+4 is directly to the right of Ctrl+_.

key sequence	displayed form	expression form
x Ctrl+& _		OverBar[x]
x Ctrl+& EscvecEsc		OverVector[x]
x Ctrl+& ~		OverTilde[x]
x Ctrl+& ^		OverHat[x]
x Ctrl+& .		OverDot[x]
x Ctrl+Shift+, _		UnderBar[x]

Ways to enter some common modifiers using control keys.

Here is

You can use

as a variable:

Non‐English Characters and Keyboards

If you enter text in languages other than English, you will typically need to use various additional accented and other characters. If your computer system is set up in an appropriate way, then you will be able to enter such characters directly using standard keys on your keyboard. But however your system is set up, the Wolfram Language always provides a uniform way to handle such characters.

	full name	alias
à	∖[AGrave]	Esca`Esc
å	∖[ARing]	EscaoEsc
ä	∖[ADoubleDot]	Esca"Esc
ç	∖[CCedilla]	Escc,Esc
č	∖[CHacek]	EsccvEsc
é	∖[EAcute]	Esce'Esc
è	∖[EGrave]	Esce`Esc
í	∖[IAcute]	Esci'Esc
ñ	∖[NTilde]	Escn~Esc
ò	∖[OGrave]	Esco`Esc

	full name	alias
ø	∖[OSlash]	Esco/Esc
ö	∖[ODoubleDot]	Esco"Esc
ù	∖[UGrave]	Escu`Esc
ü	∖[UDoubleDot]	Escu"Esc
ß	∖[SZ]	EscszEsc, EscssEsc
Å	∖[CapitalARing]	EscAoEsc
Ä	∖[CapitalADoubleDot]	EscA"Esc
Ö	∖[CapitalODoubleDot]	EscO"Esc
Ü	∖[CapitalUDoubleDot]	EscU"Esc

Some common European characters.

Here is a function whose name involves an accented character:

This is another way to enter the same input:

You should realize that there is no uniform standard for computer keyboards around the world, and as a result it is inevitable that some details of what has been said in this tutorial may not apply to your keyboard.

In particular, the identification for example of Ctrl+6 with Ctrl+^ is valid only for keyboards on which ^ appears as Shift+6. On other keyboards, the Wolfram System uses Ctrl+6 to go to a superscript position, but not necessarily Ctrl+^.

Regardless of how your keyboard is set up you can always use palettes or menu items to set up superscripts and other kinds of notation. And assuming you have some way to enter characters such as ∖, you can always give input using full names such as \[Infinity].

Other Mathematical Notation

The Wolfram Language supports an extremely wide range of mathematical notation, although often it does not assign a predefined meaning to it. Thus, for example, you can enter an expression such as x⊕y, but the Wolfram Language will not initially make any assumption about what you mean by

The Wolfram Language knows that

is an operator, but it does not initially assign any specific meaning to it:

This gives the Wolfram Language a definition for what the

operator does:

Now the Wolfram Language can evaluate

operations:

A few of the operators whose input is supported by the Wolfram Language.

The Wolfram Language assigns built‐in meanings to

and

, but not to

There are some forms which look like characters on a standard keyboard, but which are interpreted in a different way by the Wolfram Language. Thus, for example, ∖[Backslash] or Esc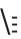

displays as ∖ but is not interpreted in the same way as a ∖ typed directly on the keyboard.

The

and

characters used here are different from the ∖ and ^ you would type directly on a keyboard:

Most operators work like

and go in between their operands. But some operators can go in other places. Thus, for example, Esc

and Esc

or ∖[LeftAngleBracket] and ∖[RightAngleBracket] are effectively operators which go around their operand.

The elements of the angle bracket operator go around their operand:

Some additional letters and letter‐like forms.

You can use letters and letter‐like forms anywhere in symbol names:

is assumed to be a symbol, and so is just multiplied by a and b:

Mixing Text and Formulas

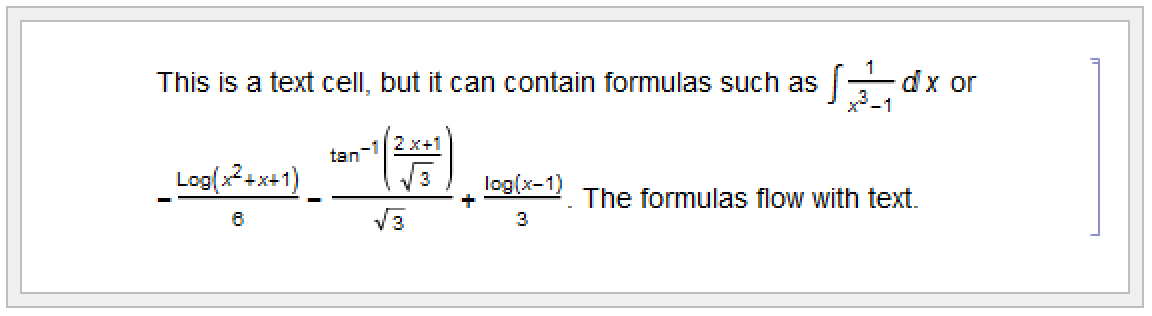
The simplest way to mix text and formulas in a Wolfram System notebook is to put each kind of material in a separate cell. Sometimes, however, you may want to embed a formula within a cell of text, or vice versa.

Ctrl+( or Ctrl+9	begin entering a formula within text, or text within a formula
Ctrl+) or Ctrl+0	end entering a formula within text, or text within a formula

Entering a formula within text, or vice versa.

Here is a notebook with formulas embedded in a text cell.

Wolfram System notebooks often contain both formulas that are intended for actual evaluation by the Wolfram Language, and ones that are intended just to be read in a more passive way.

When you insert a formula in text, you can use the Convert to StandardForm and Convert to TraditionalForm menu items within the formula to convert it to StandardForm or TraditionalForm. StandardForm is normally appropriate whenever the formula is thought of as a Wolfram System program fragment.

In general, however, you can use exactly the same mechanisms for entering formulas, whether or not they will ultimately be given as Wolfram Language input.

You should realize, however, that to make the detailed typography of typical formulas look as good as possible, the Wolfram Language automatically does things such as inserting spaces around certain operators. But these kinds of adjustments can potentially be inappropriate if you use notation in very different ways from the ones the Wolfram Language is expecting. In such cases, you may have to make detailed typographical adjustments by hand.

Displaying and Printing Wolfram System Notebooks

Depending on the purpose for which you are using a Wolfram System notebook, you may want to change its overall appearance. The front end allows you to specify independently the styles to be used for display on the screen and for printing. Typically you can do this by choosing appropriate items in the Format menu.

ScreenStyleEnvironment	styles to be used for screen display
PrintingStyleEnvironment	styles to be used for printed output
Working	standard style definitions for screen display
Presentation	style definitions for presentations
SlideShow	style definitions for displaying presentation slides
Printout	style definitions for printed output

Front end settings that define the global appearance of a notebook.

Here is a typical notebook as it appears in working form on the screen.

Here is a preview of how the notebook would appear when printed out.

Setting Up Hyperlinks

Insert ▶ Hyperlink	menu item to make the selected object a hyperlink
Hyperlink["uri"]	generate as output a hyperlink with the label and destination set as uri
Hyperlink["label","uri"]	generate as output a hyperlink with the label label and the destination uri
Hyperlink[{"file.nb",None}]	generate as output a hyperlink to the specified notebook
Hyperlink[{"file.nb","tag"}]	generate as output a hyperlink to the cell tagged as tag in the specified notebook

Methods for generating hyperlinks.

A hyperlink is a special kind of button which jumps to another part of a notebook when it is pressed. Typically hyperlinks are indicated in the Wolfram System by blue text.

To set up a hyperlink, just select the text or other object that you want to be a hyperlink. Then choose the menu item Insert ▶ Hyperlink and fill in the specification of where you want the destination of the hyperlink to be.

The destination of a hyperlink can be any standard web address (URI). Hyperlinks can also point to notebooks on the local file system, or even to specific cells inside those notebooks. Hyperlinks which point to specific cells in notebooks use cell tags to identify the cells. If a particular cell tag is used for more than one cell in a given notebook, then the hyperlink will go to the first instance of a cell with that cell tag.

A hyperlink can be generated in output by using the Wolfram Language command Hyperlink. These hyperlinks can be copied and pasted into text or used in a larger interface being generated by the Wolfram Language.

This command generates a hyperlink to the web:

Automatic Numbering

■ Choose a cell style such as DisplayFormulaNumbered.

■ Use Insert ▶ Automatic Numbering with a counter name such as Section.

Two ways to set up automatic numbering in a Wolfram System notebook.

Using the DisplayFormulaNumbered Style

These cells are in DisplayFormulaNumbered style. DisplayFormulaNumbered style is available in the default stylesheet.

Using the AutomaticNumbering Menu Item

The input for each cell here is exactly the same, but the cells contain an element that displays as a progressively larger number as one goes through the notebook.

Exposition in Wolfram System Notebooks

Wolfram System notebooks provide the basic technology that you need to be able to create a very wide range of sophisticated interactive documents. But to get the best out of this technology you need to develop an appropriate style of exposition.

Many people at first tend to use Wolfram System notebooks either as simple worksheets containing a sequence of input and output lines, or as onscreen versions of traditional books and other printed material. But the most effective and productive uses of Wolfram System notebooks tend to lie at neither one of these extremes, and instead typically involve a fine‐grained mixing of Wolfram Language input and output with explanatory text. In most cases the single most important factor in obtaining such fine‐grained mixing is uniform use of the Wolfram Language.

One might think that there would tend to be four kinds of material in a Wolfram System notebook: plain text, mathematical formulas, computer code, and interactive interfaces. But one of the key ideas of the Wolfram Language is to provide a single language that offers the best of both traditional mathematical formulas and computer code.

In StandardForm, Wolfram Language expressions have the same kind of compactness and elegance as traditional mathematical formulas. But unlike such formulas, Wolfram Language expressions are set up in a completely consistent and uniform way. As a result, if you use Wolfram Language expressions, then regardless of your subject matter, you never have to go back and reexplain your basic notation: it is always just the notation of the Wolfram Language. In addition, if you set up your explanations in terms of Wolfram Language expressions, then a reader of your notebook can immediately take what you have given, and actually execute it as Wolfram Language input.

If one has spent many years working with traditional mathematical notation, then it takes a little time to get used to seeing mathematical facts presented as StandardForm Wolfram Language expressions. Indeed, at first one often has a tendency to try to use TraditionalForm whenever possible, perhaps with hidden tags to indicate its interpretation. But quite soon one tends to evolve to a mixture of StandardForm and TraditionalForm. And in the end it becomes clear that StandardForm alone is for most purposes the most effective form of presentation.

In traditional mathematical exposition, there are many tricks for replacing chunks of text by fragments of formulas. In StandardForm many of these same tricks can be used. But the fact that Wolfram Language expressions can represent not only mathematical objects but also procedures, algorithms, graphics, and interfaces increases greatly the extent to which chunks of text can be replaced by shorter and more precise material.

Named Characters

The Wolfram System provides systemwide support for a large number of special characters. Each character has a name and a number of shortcut aliases. They are fully supported by the standard Wolfram System fonts.

Interpretation of Characters

The interpretations given here are those used in StandardForm and InputForm. Most of the interpretations also work in TraditionalForm.

You can override the interpretations by giving your own rules for MakeExpression.

Letters and letter‐like forms	used in symbol names
Infix operators	e.g.
Prefix operators	e.g.
Postfix operators	e.g.
Matchfix operators	e.g.
Compound operators	e.g.
Raw operators	operator characters that can be typed on an ordinary keyboard
Spacing characters	interpreted in the same way as an ordinary space
Structural elements	characters used to specify structure; usually ignored in interpretation
Uninterpretable elements	characters indicating missing information

Types of characters.

The precedences of operators are given in "Operator Input Forms".

Infix operators for which no grouping is specified in the listing are interpreted so that for example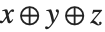

becomes CirclePlus[x,y,z].

Naming Conventions

Characters that correspond to built‐in Wolfram Language functions typically have names corresponding to those functions. Other characters typically have names that are as generic as possible.

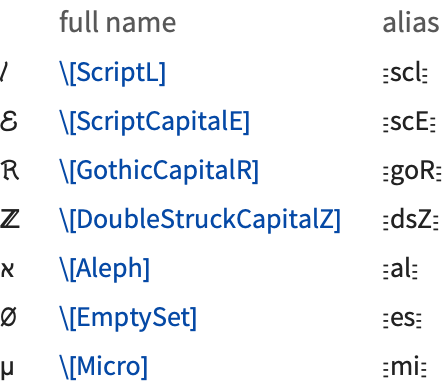
Characters with different names almost always look at least slightly different.

\[Capital…]	uppercase form of a letter
\[Left…] and \[Right…]	pieces of a matchfix operator (also arrows)
\[Raw…]	a printable ASCII character
\[…Indicator]	a visual representation of a keyboard character

Some special classes of characters.

style	Script , Gothic , etc.
variation	Curly , Gray , etc.
case	Capital , etc.
modifiers	Not , Double , Nested , etc.
direction	Left , Up , UpperRight , etc.
base	A , Epsilon , Plus , etc.
diacritical mark	Acute , Ring , etc.

Typical ordering of elements in character names.

Aliases

The Wolfram Language supports both its own system of aliases, as well as aliases based on character names in TeX and SGML or HTML. Except where they conflict, character names corresponding to plain TeX, LaTeX and AMSTeX are all supported. Note that TeX and SGML or HTML aliases are not given explicitly in the list of characters below.

EscxxxEsc	ordinary Wolfram Language alias
Esc∖xxxEsc	TeX alias
Esc&xxxEsc	SGML or HTML alias

Types of aliases.

The following general conventions are used for all aliases:

Characters that are alternatives to standard keyboard operators use these operators as their aliases (e.g. Esc->Esc for 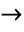, Esc&&Esc for ).
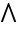Most single‐letter aliases stand for Greek letters.
Capital‐letter characters have aliases beginning with capital letters.
When there is ambiguity in the assignment of aliases, a space is inserted at the beginning of the alias for the less common character (e.g. Esc->Esc for \[Rule] and Esc␣->Esc for \[RightArrow]).
! is inserted at the beginning of the alias for a Not character.
TeX aliases begin with a backslash ∖.
SGML aliases begin with an ampersand &.
User‐defined aliases conventionally begin with a dot or comma.

Font Matching

The special fonts provided with the Wolfram System include all the characters given in this listing. Some of these characters also appear in certain ordinary text fonts.

When rendering text in a particular font, the Wolfram System notebook front end will use all the characters available in that font. It will use the special Wolfram System fonts only for other characters.

A choice is made between Times‐like, Helvetica‐like (sans serif) and Courier‐like (monospaced) variants to achieve the best matching with the ordinary text font in use.

Top

More Learning

Tech Support

Educational Programs for Adults

Educational Programs for Youth

Events

Wolfram Initiatives

Educational Resources

Hobbies & Projects

Wolfram Solutions

Wolfram Solutions For Education

Get Started

Grow Your Skills

Work with Us

Read

Educational Programs for Adults

Educational Programs for Youth

Events