WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

AdjacencyMatrix
Copy to clipboard.
✖
AdjacencyMatrix

Copy to clipboard.
✖

gives the vertex–vertex adjacency matrix of the graph g.

Copy to clipboard.
✖
AdjacencyMatrix[{vw,…}]

uses rules vw to specify the graph g.

Details

  • An adjacency matrix is also known as a connectivity matrix.
  • AdjacencyMatrix returns a SparseArray object, which can be converted to an ordinary matrix using Normal.
  • An entry aij of the adjacency matrix is the number of directed edges from vertex νi to vertex νj.
  • The diagonal entries aii count the number of loops for vertex vi.
  • An undirected edge is interpreted as two directed edges with opposite directions.
  • The vertices vi are assumed to be in the order given by VertexList[g].
  • The adjacency matrix for a graph will have dimensions 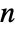×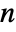, where 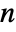is the number of vertices.

Background & Context

  • AdjacencyMatrix returns a square matrix whose rows and columns correspond to the vertices of a graph and whose elements aij are non-negative integers that give the numbers of (directed) edges from vertex vi to vertex vj. An adjacency matrix provides a useful representation of a graph that can be used to compute many properties by means of simple operations on matrices. Examples of computations on graphs that can be performed efficiently given an adjacency matrix include vertex degrees, in- and out-degrees, counts of paths between vertices in at most 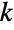steps, graph spectrum, and many others.
  • For a graph on 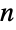vertices, the adjacency matrix has dimensions 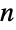×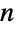. For an undirected graph, the adjacency matrix is symmetric. For a finite simple graph (i.e. an undirected, unweighted graph with no self-loops or multiple edges), the adjacency matrix must have 0s on the diagonal, and its matrix elements are given by 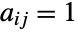if 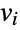is adjacent to 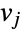and 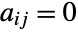otherwise.
  • An explicit adjacency matrix representation of a graph based on a particular ordering of vertices is unique. However, since the vertices of a graph may be permuted, there is a class of adjacency matrices that represents the corresponding isomorphism class of graphs. Nonetheless, the adjacency matrix for an isomorphism class is unique modulo permutation of rows and columns of the matrix (corresponding precisely to relabeling of the graph vertices).
  • AdjacencyGraph can be used to construct a graph from an adjacency matrix. IncidenceMatrix gives another matrix representation of a graph that gives vertex-edge relationships instead of vertex-vertex relationships. AdjacencyMatrix does not take graph weights into account, so WeightedAdjacencyMatrix must be used when computing the adjacency matrix of a graph having edge weights.

Examples

open allclose all

Basic Examples  (2)Summary of the most common use cases

The adjacency matrix of an undirected graph:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-dkm3wv
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-f5ppu9
Direct link to example

The adjacency matrix of a directed graph:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-pqn9g6
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-cp35xo
Direct link to example

Scope  (5)Survey of the scope of standard use cases

The adjacency matrix of an undirected graph is symmetric:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-brfunn
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-fo7txu
Direct link to example

The adjacency matrix of a directed graph can be unsymmetric:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-becm22
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-pcpon
Direct link to example

Use rules to specify the graph:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-bndh30
Direct link to example

The adjacency matrix of the graph with self-loops has diagonal entries:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-cuz87q
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-h7st8b
Direct link to example
Out[2]=2

AdjacencyMatrix works with large graphs:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-jyefgb
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-fi4a2b
Direct link to example
Out[2]=2

Use MatrixPlot to visualize the matrix:

Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-ne4gm8
Direct link to example
Out[3]=3

Applications  (7)Sample problems that can be solved with this function

Compute the degree for an undirected graph from its adjacency matrix:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-lmqwj
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-drpce4
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-c6j3u8
Direct link to example
Out[3]=3

Compute the in-degree for a directed graph from its adjacency matrix:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-6xfvz
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-gljmlv
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-dx7vu8
Direct link to example
Out[3]=3

Compute the out-degree for a directed graph from its adjacency matrix:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-dxjcn2
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-gwxjah
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-eh1ubk
Direct link to example
Out[3]=3

Count the number of paths between all vertices in exactly steps for a directed graph:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-ua4e2
Direct link to example

There are two paths from 1 to 5 in two steps:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-gqss6k
Direct link to example

Count the number of paths from to in exactly steps for a directed graph:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-foetn5
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-euhrnb
Direct link to example
Out[2]=2

Compute the co-citation matrix, where the co-citation for two vertices is the number of common ancestors:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-j2ewr1
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-jw9lr9
Direct link to example
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-t2ane
Direct link to example

The co-citation between and :

Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-ikfkct
Direct link to example
Out[4]=4

Compute the coupling matrix, where the coupling between two vertices is the number of common descendants:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-bf264s
Direct link to example
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-sycjs
Direct link to example
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-bkutjf
Direct link to example

The coupling between and :

Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-k3mzv
Direct link to example
Out[4]=4

Properties & Relations  (14)Properties of the function, and connections to other functions

Rows and columns of the adjacency matrix follow the order given by VertexList:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-joylju
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-cwu88m
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-i573me
Direct link to example

Use VertexIndex to find the matrix row and column corresponding to a pair of vertices:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-6ugpls
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-59k8ql
Direct link to example

Check whether 1 and 4 are adjacent vertices:

Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-fdamdx
Direct link to example
Out[3]=3

Compare with EdgeQ:

Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-smxblt
Direct link to example
Out[4]=4

An undirected graph has a symmetric adjacency matrix:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-tt62l
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-iotp57
Direct link to example
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-dnnjjc
Direct link to example
Out[3]=3

Use AdjacencyGraph to construct a graph from an adjacency matrix:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-clncmi
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-p3vm2
Direct link to example
Out[2]=2

The main diagonal of the adjacency matrix for any graph without loops has all zero entries:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-jez1rj
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-ddcmod
Direct link to example
Out[2]=2

The number of rows or columns of the adjacency matrix is equal to the number of vertices:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-dxrnuc
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-gmegrm
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-b6qsb8
Direct link to example
Out[3]=3

Isomorphic graphs can have different adjacency matrices:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-gr1h2g
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-e26sju
Direct link to example
Out[2]=2
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-m4mylm
Direct link to example
Out[3]=3

Permute the adjacency matrix of g according to the mapping that gets an equal matrix of h:

Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-rylue0
Direct link to example
Out[4]=4
Copy to clipboard.
In[5]:=5
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-7hhmw
Direct link to example
Out[5]=5

A d-regular graph g is connected if the multiplicity of its d eigenvalue is 1:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-ofkze6
Direct link to example
Out[1]=1

The graph is 3-regular:

Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-jzz0z2
Direct link to example
Out[2]=2

The multiplicity 3 is 1, so it is connected:

Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-chrwal
Direct link to example
Out[3]=3
Copy to clipboard.
In[4]:=4
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-bdi8ze
Direct link to example
Out[4]=4

For a complete graph, all entries outside the diagonal are 1s in the adjacency matrix:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-ibess
Direct link to example
Out[1]=1

A complete -partite graph has zero diagonal block entries:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-k4sdai
Direct link to example
Out[1]=1

A TuranGraph is bipartite:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-dm7609
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-e5s3uc
Direct link to example
Out[2]=2

A StarGraph has 1s in the first column and first row only:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-d7ifij
Direct link to example
Out[1]=1

For a path, rows of an adjacency matrix will contain one or two elements:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-n7ss2q
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-e77b1
Direct link to example
Out[2]=2

The adjacency matrix of a line graph can be computed by its IncidenceMatrix:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-pgy1sf
Direct link to example
Out[1]=1
Copy to clipboard.
In[2]:=2
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-cv94r3
Direct link to example
Copy to clipboard.
In[3]:=3
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-ergbug
Direct link to example
Out[3]=3

Possible Issues  (1)Common pitfalls and unexpected behavior

An empty graph has no adjacency matrix:

Copy to clipboard.
In[1]:=1
✖
https://wolfram.com/xid/0hyvz9euu3xn7vy6-3r3s
Direct link to example
Out[1]=1
Wolfram Research (2010), AdjacencyMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/AdjacencyMatrix.html (updated 2015).
Copy to clipboard.
✖
Wolfram Research (2010), AdjacencyMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/AdjacencyMatrix.html (updated 2015).

Text

Wolfram Research (2010), AdjacencyMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/AdjacencyMatrix.html (updated 2015).

Copy to clipboard.
✖
Wolfram Research (2010), AdjacencyMatrix, Wolfram Language function, https://reference.wolfram.com/language/ref/AdjacencyMatrix.html (updated 2015).

CMS

Wolfram Language. 2010. "AdjacencyMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/AdjacencyMatrix.html.

Copy to clipboard.
✖
Wolfram Language. 2010. "AdjacencyMatrix." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/AdjacencyMatrix.html.

APA

Wolfram Language. (2010). AdjacencyMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AdjacencyMatrix.html

Copy to clipboard.
✖
Wolfram Language. (2010). AdjacencyMatrix. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/AdjacencyMatrix.html

BibTeX

@misc{reference.wolfram_2025_adjacencymatrix, author="Wolfram Research", title="{AdjacencyMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/AdjacencyMatrix.html}", note=[Accessed: 04-April-2025 ]}

Copy to clipboard.
✖
@misc{reference.wolfram_2025_adjacencymatrix, author="Wolfram Research", title="{AdjacencyMatrix}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/AdjacencyMatrix.html}", note=[Accessed: 04-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_adjacencymatrix, organization={Wolfram Research}, title={AdjacencyMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/AdjacencyMatrix.html}, note=[Accessed: 04-April-2025 ]}

Copy to clipboard.
✖
@online{reference.wolfram_2025_adjacencymatrix, organization={Wolfram Research}, title={AdjacencyMatrix}, year={2015}, url={https://reference.wolfram.com/language/ref/AdjacencyMatrix.html}, note=[Accessed: 04-April-2025 ]}