Chebyshev2FilterModel

Chebyshev2FilterModel[n]

creates a lowpass Chebyshev type 2 filter of order n.

Chebyshev2FilterModel[{n,ωc}]

uses the cutoff frequency ωc.

Chebyshev2FilterModel[{"type",spec}]

uses the full filter specification {"type",spec}.

Chebyshev2FilterModel[{"type",spec},var]

expresses the model in terms of the variable var.

Details

  • Chebyshev2FilterModel returns the filter as a TransferFunctionModel.
  • Chebyshev2FilterModel[{n,ω}] returns a lowpass filter with attenuation of 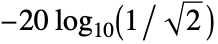(approximately 3 dB) at frequency ω.
  • Chebyshev2FilterModel[n] uses the cutoff frequency of 1.
  • Filter specification {"type",spec} can be any of the following:
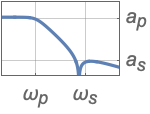
  • {"Lowpass",{ωp,ωs},{ap,as}}lowpass filter using passband and stopband frequencies and attenuations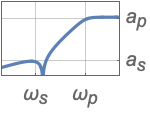
    {"Highpass",{ωs,ωp},{as,ap}}highpass filter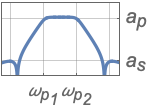
    {"Bandpass",{ωs1,ωp1,ωp2,ωs2},{as,ap}}bandpass filter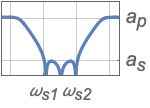
    {"Bandstop",{ωp1,ωs1,ωs2,ωp2},{ap,as}}bandstop filter
  • Frequency values should be given in an ascending order.
  • Values ap and as are respectively absolute values of passband and stopband attenuations.
  • Given a gain fraction 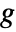, the attenuation is .

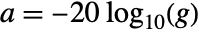Examples

open allclose all

Basic Examples  (1)

A Chebyshev type 2 filter model:

Bode plot of the modeled filter:

Scope  (7)

A symbolic representation of an order 2 lowpass filter:

Exact computation of the model:

Computation of the model with precision 24:

Create a filter model using the variable s:

Create a lowpass Chebyshev type 2 filter:

Create a highpass Chebyshev type 2 filter:

Create a bandpass Chebyshev type 2 filter:

Create a bandstop Chebyshev type 2 filter:

Applications  (6)

Create a lowpass Chebyshev type 2 filter:

Filter out high-frequency noise from a sinusoidal signal:

Chebyshev type 2 filter phase shifts the response by Arg[tf[ω ]], where ω is the frequency of the input sinusoid:

Correct for the phase shift:

Create a highpass Chebyshev type 2 filter from the lowpass prototype:

Filter out low-frequency sinusoid from the input:

Design a digital FIR lowpass filter using the Chebyshev 2 approximation that satisfies the following passband and stopband frequencies and attenuations:

Obtain the equivalent analog frequencies, assuming a sampling period of 1:

Compute the analog Chebyshev 1 transfer function:

Convert to discrete-time model:

Create an FIR approximation of a discrete-time Chebyshev type 2 IIR filter.

Implement a lowpass digital Chebyshev type 2 filter:

Obtain the impulse response of the IIR filter and evaluate for the desired number of samples:

Plot the FIR filter:

Smooth financial data using an FIR approximation of a Chebyshev filter:

Filter an image using a lowpass Chebyshev type 2 filter:

Filter an image using a highpass Chebyshev type 2 filter:

Properties & Relations  (5)

Compare Chebyshev type 1 and type 2 lowpass filters:

Extract the order of the Chebyshev type 2 polynomial:

Find the poles and zeros of a Chebyshev type 2 filter:

Plot poles and zeros of the Chebyshev filter:

Implement a lowpass digital Chebyshev type 2 filter:

Plot poles and zeros of the digital Chebyshev type 2 filter:

Convert a lowpass filter to high pass:

Possible Issues  (1)

A symbolic filter cannot be returned with full specification since the order is not computable:

Wolfram Research (2012), Chebyshev2FilterModel, Wolfram Language function, https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html.

Text

Wolfram Research (2012), Chebyshev2FilterModel, Wolfram Language function, https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html.

CMS

Wolfram Language. 2012. "Chebyshev2FilterModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html.

APA

Wolfram Language. (2012). Chebyshev2FilterModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html

BibTeX

@misc{reference.wolfram_2024_chebyshev2filtermodel, author="Wolfram Research", title="{Chebyshev2FilterModel}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_chebyshev2filtermodel, organization={Wolfram Research}, title={Chebyshev2FilterModel}, year={2012}, url={https://reference.wolfram.com/language/ref/Chebyshev2FilterModel.html}, note=[Accessed: 30-December-2024 ]}