DedekindEta

DedekindEta[τ]

gives the Dedekind eta modular elliptic function TemplateBox[{tau}, DedekindEta].

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • DedekindEta is defined only in the upper half of the complex τ plane. It is not defined for real τ.
  • The argument τ is the ratio of Weierstrass half‐periods .
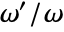  • DedekindEta satisfies 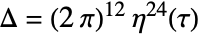where 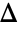is the discriminant, given in terms of Weierstrass invariants by .
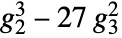  • For certain special arguments, DedekindEta automatically evaluates to exact values.
  • DedekindEta can be evaluated to arbitrary numerical precision.
  • DedekindEta automatically threads over lists.
  • DedekindEta can be used with CenteredInterval objects. »

Examples

open allclose all

Basic Examples  (2)

Evaluate numerically:

Plot over a subset of the reals:

Scope  (14)

Numerical Evaluation  (4)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Evaluate efficiently at high precision:

DedekindEta can be used with CenteredInterval objects:

Specific Values  (2)

Value at fixed point:

DedekindEta threads elementwise over lists:

Visualization  (2)

Plot the DedekindEta function for various parameters:

Plot the real part of the DedekindEta function in three dimensions:

Plot the imaginary part of the DedekindEta function in three dimensions:

Function Properties  (6)

Complex domain of DedekindEta:

DedekindEta is a periodic function:

DedekindEta is an analytic function on its domain:

It is not an entire function, however:

It has both singularities and discontinuities:

DedekindEta is not injective over the complexes:

DedekindEta is not surjective:

TraditionalForm formatting:

Applications  (3)

The modular discriminant at I is given by DedekindEta:

Compare with the general definition:

Plot the DedekindEta function in the upper half of the complex plane:

The modular discriminant:

Relation with DedekindEta:

Properties & Relations  (2)

Machine-precision input is insufficient to give a correct answer:

With exact input, the answer is correct:

Because DedekindEta is a numerical function with numeric arguments, it might be considered a numeric quantity but because of its boundary of analyticity, it might not be evaluatable to a number:

Wolfram Research (1996), DedekindEta, Wolfram Language function, https://reference.wolfram.com/language/ref/DedekindEta.html (updated 2021).

Text

Wolfram Research (1996), DedekindEta, Wolfram Language function, https://reference.wolfram.com/language/ref/DedekindEta.html (updated 2021).

CMS

Wolfram Language. 1996. "DedekindEta." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/DedekindEta.html.

APA

Wolfram Language. (1996). DedekindEta. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DedekindEta.html

BibTeX

@misc{reference.wolfram_2025_dedekindeta, author="Wolfram Research", title="{DedekindEta}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/DedekindEta.html}", note=[Accessed: 24-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_dedekindeta, organization={Wolfram Research}, title={DedekindEta}, year={2021}, url={https://reference.wolfram.com/language/ref/DedekindEta.html}, note=[Accessed: 24-April-2025 ]}