designs a lowpass elliptic filter of order n.
EllipticFilterModel[{n,ωc}]
uses the cutoff frequency ωc.
EllipticFilterModel[{"type",spec}]
designs an elliptic filter of the specified type "type", using the spec.
EllipticFilterModel[{"type",spec},var]
expresses the model in terms of the variable var.


EllipticFilterModel
designs a lowpass elliptic filter of order n.
EllipticFilterModel[{n,ωc}]
uses the cutoff frequency ωc.
EllipticFilterModel[{"type",spec}]
designs an elliptic filter of the specified type "type", using the spec.
EllipticFilterModel[{"type",spec},var]
expresses the model in terms of the variable var.
Details

- EllipticFilterModel returns the designed filter as a TransferFunctionModel.
- EllipticFilterModel[{n,ω}] returns a lowpass filter with attenuation of
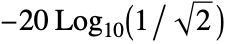 (approximately 3 dB) at frequency ω.
(approximately 3 dB) at frequency ω. - EllipticFilterModel[n] uses the cutoff frequency of 1.
- Filter specification {"type",spec} can be any of the following:
-
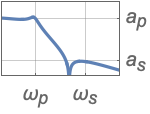
{"Lowpass",{ωp,ωs},{ap,as}} lowpass filter using passband and stopband frequencies and attenuations 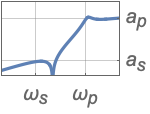
{"Highpass",{ωs,ωp},{as,ap}} highpass filter 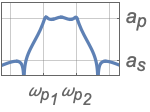
{"Bandpass",{ωs1,ωp1,ωp2,ωs2},{as,ap}} bandpass filter 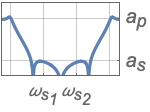
{"Bandstop",{ωp1,ωs1,ωs2,ωp2},{ap,as}} bandstop filter - Frequency values should be given in an ascending order.
- Values ap and as are absolute values of passband and stopband attenuations, respectively.
- Given a gain fraction
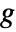 , the attenuation is
, the attenuation is 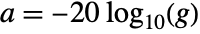 .
.
Examples
open all close allBasic Examples (2)
Scope (8)
A symbolic representation of an order 2 lowpass filter:
Exact computation of the model:
Computation of the model with precision 24:
Create a filter model using the variable s:
Create a lowpass filter model with a cutoff frequency of 10:
Create a lowpass elliptic filter:
Create a highpass elliptic filter:
Applications (6)
Create a lowpass elliptic filter:
Filter out high-frequency noise from a sinusoidal signal:
Elliptic filter phase shifts the response by Arg[tf[ω ]], where ω is the frequency of the input sinusoid:
Create a highpass elliptic filter from the lowpass prototype:
Filter out low-frequency sinusoid from the input:
Design a digital lowpass filter using the elliptic approximation that satisfies the following passband and stop-band frequencies and attenuations:
Obtain the equivalent analog frequencies assuming a sampling period of 1:
Compute the analog elliptic filter transfer function:
Convert to discrete-time model:
Create an FIR approximation of a discrete-time elliptic IIR filter.
Implement a lowpass digital elliptic filter:
Obtain the desired number of FIR samples from the impulse response of the discrete-time elliptic filter:
Smooth financial data using an FIR approximation of an elliptic filter:
Related Guides
History
Text
Wolfram Research (2012), EllipticFilterModel, Wolfram Language function, https://reference.wolfram.com/language/ref/EllipticFilterModel.html.
CMS
Wolfram Language. 2012. "EllipticFilterModel." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EllipticFilterModel.html.
APA
Wolfram Language. (2012). EllipticFilterModel. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EllipticFilterModel.html
BibTeX
@misc{reference.wolfram_2025_ellipticfiltermodel, author="Wolfram Research", title="{EllipticFilterModel}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/EllipticFilterModel.html}", note=[Accessed: 11-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_ellipticfiltermodel, organization={Wolfram Research}, title={EllipticFilterModel}, year={2012}, url={https://reference.wolfram.com/language/ref/EllipticFilterModel.html}, note=[Accessed: 11-March-2026]}