 |
BUILT-IN MATHEMATICA SYMBOL
Erosion[image, ker]
gives the morphological erosion of image with respect to the structuring element ker.
Erosion[image, r]
gives the erosion with respect to a range-r square.
Erosion[data, ...]
applies erosion to an array of data.
Details and Options
- Erosion works with binary, grayscale, and other images.
- Erosion works with 3D as well as 2D images, and also with data arrays of any rank.
- The structuring element ker is a matrix containing
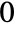s and 
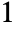s. - Erosion automatically adds zeros to structuring elements so that they have odd dimensions.
- Erosion[image, r] is equivalent to Erosion[image, BoxMatrix[r]].
- If multiple image channels are present, Erosion operates on each of them separately.
- Erosion takes a Padding option that specifies the values to assume for pixels outside the image.
- The default setting is Padding->1, corresponding to pixel value
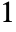for all channels. - Erosion[image, ker] interprets the structuring element so that Erosion[image, {{0, 0, 1}}] translates the image to the left.
New in 7 | Last modified in 9
