Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

EulerPhi

gives the Euler totient function .

Details

EulerPhi is also known as the Euler totient function or phi function.
Integer mathematical function, suitable for both symbolic and numerical manipulation.
Typically used in cryptography and in many applications in elementary number theory.
EulerPhi[n] counts positive integers up to n that are relatively prime to n.
For a number 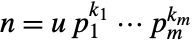with 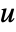a unit and 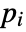primes, EulerPhi[n] gives .

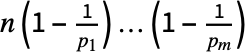Examples

open allclose all

Basic Examples (2)

Compute the Euler totient function of 10:

Plot the sequence:

Scope (9)

Numerical Evaluation (4)

Compute using integers:

Compute for large arguments:

EulerPhi threads over lists:

TraditionalForm formatting:

Symbolic Manipulation: (5)

Solve equations involving EulerPhi:

Use FullSimplify with EulerPhi:

Use FunctionExpand with EulerPhi:

FindSequenceFunction can recognize the EulerPhi sequence:

DirichletTransform:

Applications (9)

Basic Applications (4)

Find integers n such that :

Length of the n^th-order FareySequence can be expressed in terms of EulerPhi:

Power series of the generating function for GCD:

Count the number of primes using EulerPhi:

Number Theory (5)

Model Fleck's totient function:

reproduces the Euler totient function:

Generalizations and closed forms:

Plot the cumulative sum of EulerPhi:

Compare with an asymptotic approximation:

First several -s where the difference $sum_(n=1)^kTemplateBox[{n}, EulerPhi]-3 k^2/pi^2$ is negative:

The probability that two randomly chosen positive integers less than x are relatively prime:

Compare with the asymptotic limit:

Build RSA-like encryption scheme. Start with the modulus:

Find the universal exponent of the multiplication group modulo n:

Private key:

Public key:

Encrypt a message:

Decrypt it:

Number of cyclic necklaces of length n that can be formed with b types of beads:

Properties & Relations (11)

EulerPhi is non-negative:

EulerPhi is a multiplicative function:

For any prime number p and natural number r, ϕ(p^r)=p^r-p^r-1:

Similarly, EulerPhi[n]==n∏_p|n(1-1/p) where p is prime:

Alternatively, EulerPhi[n]==n∑_k|nMoebiusMu[k]/k:

CarmichaelLambda divides EulerPhi:

When n is a prime power, they are equal:

Show that ϕ(d)=n:

For a Cyclotomic field, the NumberFieldDiscriminant can be found using EulerPhi:

If has a primitive root, then CarmichaelLambda and EulerPhi are the same:

Determine EulerPhi through prime factorization:

For any square-free number n, the totient of n is equal to the product of the totients of each factor of n :

Possible Issues (1)

Value at 0:

Neat Examples (4)

Form an absolutely abnormal number as the limit of the following sequence:

Digits of the sixth approximation in various bases:

Iterate the map and display result modulo :

The only 8 solutions of :

Plot of Ulam spiral where numbers are colored based on the values of EulerPhi:

Top