Built-in Mathematica Symbol

LinearProgramming

LinearProgramming[c, m, b]
finds a vector x which minimizes the quantity c.x subject to the constraints m.x≥b and x≥0.

LinearProgramming[c, m, {{b₁, s₁}, {b₂, s₂}, ...}]
finds a vector x which minimizes c.x subject to x≥0 and linear constraints specified by the matrix m and the pairs {b_i, s_i}. For each row m_i of m, the corresponding constraint is m_i.x≥b_i if s_i

1, or m_i.x

b_i if s_i

0, or m_i.x≤b_i if s_i

-1.

LinearProgramming[c, m, b, l]
minimizes c.x subject to the constraints specified by m and b and x≥l.

LinearProgramming[c, m, b, {l₁, l₂, ...}]
minimizes c.x subject to the constraints specified by m and b and x_i≥l_i.

LinearProgramming[c, m, b, {{l₁, u₁}, {l₂, u₂}, ...}]
minimizes c.x subject to the constraints specified by m and b and l_i≤x_i≤u_i.

LinearProgramming[c, m, b, lu, dom]
takes the elements of x to be in the domain dom, either Reals or Integers.

LinearProgramming[c, m, b, lu, {dom₁, dom₂, ...}]
takes x_i to be in the domain dom_i.

MORE INFORMATION

All entries in the vectors c and b and the matrix m must be real numbers.

The bounds l_i and u_i must be real numbers or Infinity or -Infinity.

None is equivalent to specifying no bounds.

LinearProgramming gives exact rational number or integer results if its input consists of exact rational numbers.

LinearProgramming returns unevaluated if no solution can be found.

LinearProgramming finds approximate numerical results if its input contains approximate numbers. The option Tolerance specifies the tolerance to be used for internal comparisons. The default is Tolerance->Automatic, which does exact comparisons for exact numbers, and uses tolerance 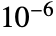for approximate numbers.