LocationEquivalenceTest

LocationEquivalenceTest[{data₁,data₂,…}]

tests whether the means or medians of the data_i are equal.

LocationEquivalenceTest[{data₁,…},"property"]

returns the value of "property".

Details and Options

LocationEquivalenceTest performs a hypothesis test on the data_i with null hypothesis 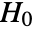that the true location parameters of the populations are equal, 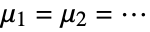, and alternative hypothesis 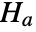that at least one is different.
By default, a probability value or 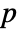-value is returned.
A small 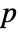-value suggests that it is unlikely that 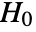is true.
The data_i must be univariate {x₁,x₂,…}.
LocationEquivalenceTest[{data₁,…}] will choose the most powerful test that applies to the data.
LocationEquivalenceTest[{data₁,…},All] will choose all tests that apply to the data.
LocationEquivalenceTest[{data₁,…},"test"] reports the 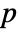-value according to "test".
Mean-based tests assume that the data_i are normally distributed. The median-based Kruskal–Wallis test assumes that data_i are symmetric about a common median. The complete block 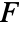and Friedman rank tests assume that the data is in randomized complete blocks. All of the tests require the data_i to have equal variances.
The following tests can be used:

"CompleteBlockF"	normality, blocked	mean test for complete block design
"FriedmanRank"	blocked	median test for complete block design
"KruskalWallis"	symmetry	median test for two or more samples
"KSampleT"	normality	mean test for two or more samples

The complete block 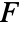test effectively performs one-way analysis of variance for randomized complete block design.
The Friedman rank test ranks observations across rows and sums the ranks along columns in the data to arrive at the test statistic. The statistic is corrected for ties.
The Kruskal–Wallis test effectively performs a one-way analysis of variance on the ranks of the data. The test statistic is corrected for ties.
The 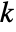-sample 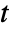-test is equivalent to a one-way analysis of variance of the data.
LocationEquivalenceTest[{data₁,…},"HypothesisTestData"] returns a HypothesisTestData object htd that can be used to extract additional test results and properties using the form htd["property"].
LocationEquivalenceTest[{data₁,…},"property"] can be used to directly give the value of "property".
Properties related to the reporting of test results include:

	"AllTests"	list of all applicable tests
	"AutomaticTest"	test chosen if Automatic is used
	"DegreesOfFreedom"	the degrees of freedom used in a test
	"PValue"	list of 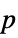-values
	"PValueTable"	formatted table of 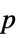-values
	"ShortTestConclusion"	a short description of the conclusion of a test
	"TestConclusion"	a description of the conclusion of a test
	"TestData"	list of pairs of test statistics and 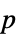-values
	"TestDataTable"	formatted table of 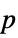-values and test statistics
	"TestStatistic"	list of test statistics
	"TestStatisticTable"	formatted table of test statistics

The following options can be given:

Method	Automatic	the method to use for computing 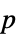-values
SignificanceLevel	0.05	cutoff for diagnostics and reporting
VerifyTestAssumptions	Automatic	what assumptions to verify

For tests of location, a cutoff 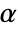is chosen such that 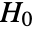is rejected only if 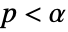. The value of 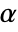used for the "TestConclusion" and "ShortTestConclusion" properties is controlled by the SignificanceLevel option. This value 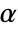is also used in diagnostic tests of assumptions, including tests for normality, equal variance, and symmetry. By default, 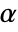is set to 0.05.
Named settings for VerifyTestAssumptions in LocationEquivalenceTest include:

	"Normality"	verify that all data is normally distributed
	"EqualVariance"	verify that the data_i have equal variances
	"Symmetry"	verify symmetry about a common median

Examples

open allclose all

Basic Examples (3)

Test whether the means or medians from two or more populations are all equivalent:

Create a HypothesisTestData object for repeated property extraction:

The complete block test can be used to test for mean differences with complete block design:

There is a significant difference among the means at the 0.05 level:

Use the Friedman rank test to test for differences in medians with complete block design:

It appears that at least one median differs significantly from the others:

Scope (9)

Testing (5)

Perform a particular test for equal locations:

Any number of tests can be performed simultaneously:

Perform all tests appropriate to the data simultaneously:

Use the property "AllTests" to identify which tests were used:

Create a HypothesisTestData object for repeated property extraction:

The properties available for extraction:

Extract some properties from a HypothesisTestData object:

The -value and test statistic from a -sample -test:

Extract any number of properties simultaneously:

The -value and test statistic from a Kruskal–Wallis test:

Reporting (4)

Tabulate the results from a selection of tests:

A full table of all appropriate test results:

A table of selected test results:

Retrieve the entries from a test table for customized reporting:

The -values are above 0.05, so there is not enough evidence to reject at that level:

Tabulate -values for a test or group of tests:

The -value from the table:

A table of -values from all appropriate tests:

A table of -values from a subset of tests:

Report the test statistic from a test or group of tests:

The test statistic from the table:

A table of test statistics from all appropriate tests:

Options (8)

Method (2)

Compute the Kruskal–Wallis test for a group of datasets:

The rescaled test statistic follows an FRatioDistribution:

Use the asymptotic chi-square approximation:

Use the asymptotic chi-square distribution for the Friedman rank test:

By default, Conover's -distribution approximation is used:

SignificanceLevel (3)

Set the significance level for diagnostic tests:

The default level is 0.05:

Setting the significance level may alter which test is automatically chosen:

A median-based test would have been chosen by default:

The significance level is also used for "TestConclusion" and "ShortTestConclusion":

VerifyTestAssumptions (3)

Diagnostics can be controlled as a group using All or None:

Verify all assumptions:

Check no assumptions:

Diagnostics can be controlled independently:

Assume normality but check for symmetry:

Only check for normality:

Test assumption values can be explicitly set:

The Kruskal-Wallis test was previously chosen because the data is not normally distributed:

Applications (4)

Test whether a group of populations shares a common location:

The first group of datasets was drawn from populations with very different locations:

Populations represented by the second group all have similar locations:

Morphological measures of two crab varieties were taken for each of the two sexes. Determine whether the measures differ across the various groups:

The rear width is the only measure that differs by gender when variety is ignored:

All measures are significantly different when gender and variety are considered simultaneously:

A pilot study was conducted for 75 patients with type II diabetes who had failed to achieve target weight loss with a particular medication. The patients were randomly assigned to three groups: a control group continuing the original medication, and two treatment groups that received 50 and 100 mg of a new medication, respectively. Weight loss in pounds over a 12-week period was recorded:

There is a significant difference in the means of the groups:

Using a Bonferroni correction in a test of each pairwise difference shows that both treatment levels perform better than the control, but that they are not significantly different from one another:

A group of six food critics rated four restaurants for quality on a 100-point scale. Determine whether there is a significant difference in the quality of the restaurants according to critics:

Bar charts of the median score by critic:

Bar charts of the median score for each restaurant:

Accounting for the blocked structure, a significant difference in quality can be detected:

Properties & Relations (12)

The -value returned by a -sample -test is equivalent to that of TTest for two samples:

The Kruskal–Wallis test is a -sample extension of the two-sample Mann–Whitney test:

The Mann–Whitney -value is corrected for continuity and ties:

Under the -sample -test statistic follows an FRatioDistribution[g-1,n-g], where g is the number of datasets and n is the total number of observations: