MathieuCharacteristicA

MathieuCharacteristicA[r,q]

gives the characteristic value for even Mathieu functions with characteristic exponent r and parameter q.

Details

  • Mathematical function, suitable for both symbolic and numerical manipulation.
  • The characteristic value 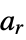gives the value of the parameter 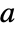in 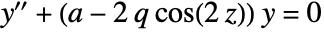for which the solution has the form 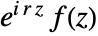, where 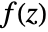is an even function of 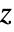with period .
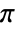  • For certain special arguments, MathieuCharacteristicA automatically evaluates to exact values.
  • MathieuCharacteristicA can be evaluated to arbitrary numerical precision.
  • MathieuCharacteristicA automatically threads over lists.

Examples

open allclose all

Basic Examples  (3)

Evaluate numerically:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Scope  (20)

Numerical Evaluation  (6)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

Compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix MathieuCharacteristicA function using MatrixFunction:

Specific Values  (2)

Simple exact values are generated automatically:

Find the positive maximum of MathieuCharacteristicA[2,q ]:

Visualization  (3)

Plot the MathieuCharacteristicA function for integer parameters:

Plot the MathieuCharacteristicA function for noninteger parameters:

Plot the real part of MathieuCharacteristicA:

Plot the imaginary part of MathieuCharacteristicA:

Function Properties  (7)

The real domain of MathieuCharacteristicA:

Approximate function range of TemplateBox[{1, x}, MathieuCharacteristicA]:

TemplateBox[{1, x}, MathieuCharacteristicA] is a continuous function of :

TemplateBox[{1, x}, MathieuCharacteristicA] is neither non-increasing nor non-decreasing:

TemplateBox[{1, x}, MathieuCharacteristicA] is not injective:

MathieuCharacteristicA threads elementwise over lists:

TraditionalForm formatting:

Series Expansions  (2)

Find the Taylor expansion using Series:

Plots of the first three approximations around :

Find the series expansion at infinity:

Applications  (4)

Symmetric periodic solutions of the Mathieu differential equation:

This shows the stability diagram for the Mathieu equation:

As a function of the first argument, MathieuCharacteristicA is a piecewise continuous function (called bands and band gaps in solid state physics):

Solve the Laplace equation in an ellipse using separation of variables:

This finds a zero:

This plots an eigenfunction. It vanishes at the ellipse boundary:

Properties & Relations  (1)

MathieuCharacteristicA is a special case of SpheroidalEigenvalue:

Neat Examples  (1)

Branch points of the Mathieu characteristic along the imaginary q axis:

Wolfram Research (1996), MathieuCharacteristicA, Wolfram Language function, https://reference.wolfram.com/language/ref/MathieuCharacteristicA.html.

Text

Wolfram Research (1996), MathieuCharacteristicA, Wolfram Language function, https://reference.wolfram.com/language/ref/MathieuCharacteristicA.html.

CMS

Wolfram Language. 1996. "MathieuCharacteristicA." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/MathieuCharacteristicA.html.

APA

Wolfram Language. (1996). MathieuCharacteristicA. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MathieuCharacteristicA.html

BibTeX

@misc{reference.wolfram_2024_mathieucharacteristica, author="Wolfram Research", title="{MathieuCharacteristicA}", year="1996", howpublished="\url{https://reference.wolfram.com/language/ref/MathieuCharacteristicA.html}", note=[Accessed: 04-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_mathieucharacteristica, organization={Wolfram Research}, title={MathieuCharacteristicA}, year={1996}, url={https://reference.wolfram.com/language/ref/MathieuCharacteristicA.html}, note=[Accessed: 04-November-2024 ]}