PIDTune
Details and Options
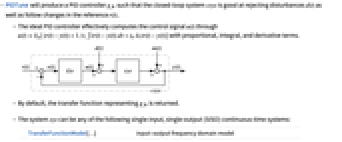








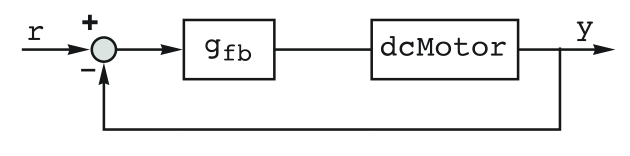
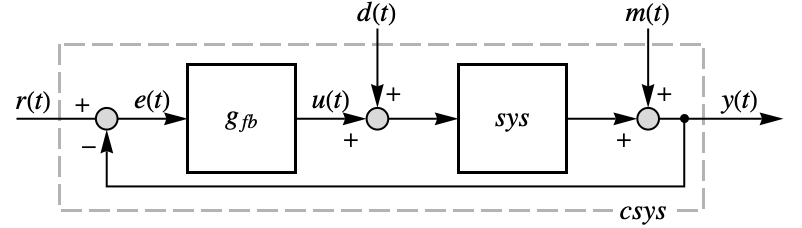
- PIDTune will produce a PID controller gfb such that the closed-loop system csys is good at rejecting disturbances
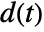 as well as follow changes in the reference
as well as follow changes in the reference 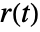 .
. - The ideal PID controller effectively computes the control signal
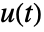 through
through 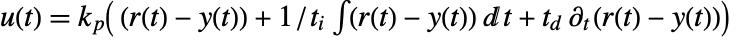 with proportional, integral, and derivative terms.
with proportional, integral, and derivative terms. - By default, the transfer function representing gfb is returned.
- The system sys can be any of the following single-input, single-output (SISO) continuous-time systems:
-
TransferFunctionModel[…] input-output frequency domain model StateSpaceModel[…] linear control input and linear state AffineStateSpaceModel[…] linear control input and nonlinear state NonlinearStateSpaceModel[…] nonlinear control input and nonlinear state SystemModel[…] general system model - For nonlinear systems such as AffineStateSpaceModel, NonlinearStateSpaceModel and SystemModel, the system will be linearized around its stored operating point.
- PIDTune is a SISO controller design technique. PIDTune[sspec,…] can be used to specify the SISO subsystem of a multiple-input, multiple-output system.
- The system specification sspec is an Association that can have the following keys:
-
"InputModel" input model sys "FeedbackInput" feedback input of sys "MeasuredOutput" measured output of sys - The following controller architectures "carch" can be used:
-
"P" proportional "PI" proportional integral "PD" proportional derivative "PID" proportional integral derivative "PFD" "PD" with filtered derivative part "PIFD" "PID" with filtered derivative part - By default, a "PI" controller is chosen.
- The tuning rule "trule" is chosen automatically, unless explicitly specified, based on stability properties of the system sys.
- The following tuning rules "trule" can be used:
-
"AMIGO" approximate 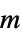 -constrained integral gain optimization
-constrained integral gain optimization"AMIGOFrequency" "AMIGO" from frequency response "ChienHronesReswick" uses rules based on step response "CohenCoon" dominant pole placement for amplitude decay ratio 0.25 "DisturbanceRejection" minimizes infinity norm of disturbance response "ErrorIntegral" minimizes an integral of error 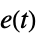
"KappaTau" dominant pole placement "KappaTauFrequency" dominant pole placement from frequency response "LambdaTuning" uses internal model control "LoopShaping" exact "AMIGO" "SkogestadIMC" uses internal model control based on half-rule reduction "TyreusLuyben" uses rules based on frequency response "ZieglerNichols" uses rules based on step response "ZieglerNicholsFrequency" uses rules based on frequency response - PIDTune[sys,…,"Data"] returns a SystemsModelControllerData object cd that can be used to extract additional properties using the form cd["prop"].
- PIDTune[sys,…,"prop"] can be used to directly give the value of cd["prop"].
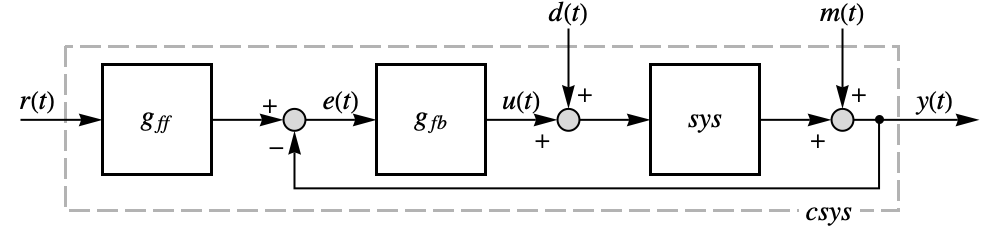
- PIDTune can optionally compute a feedforward filter gff to improve tracking of the reference
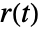 independently of disturbance rejection capabilities of the feedback controller gfb.
independently of disturbance rejection capabilities of the feedback controller gfb. - The feedforward weights b and c affect what fraction of the reference signal
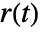 is provided to the different terms of the PID controller. The resulting controller is effectively given by
is provided to the different terms of the PID controller. The resulting controller is effectively given by 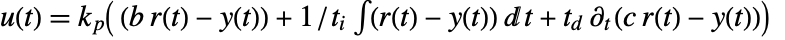 , but provided as a separate feedforward filter gff having same effect when combined with the feedback controller gfb.
, but provided as a separate feedforward filter gff having same effect when combined with the feedback controller gfb. - Properties related to different transfer functions include:
-
"Feedback" feedback gfb "Feedforward" feedforward gff "OpenLoop" series connection of gfb and sys "DisturbanceOutput" transfer function from 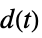 to
to 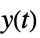
"DisturbanceControl" transfer function from 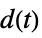 to
to 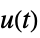
"ReferenceOutput" transfer function from 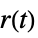 to
to 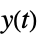
"ReferenceControl" transfer function from 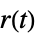 to
to 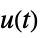
"SensorOutput" transfer function from 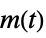 to
to 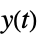
"SensorControl" transfer function from 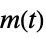 to
to 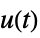
"ISA" transfer function from 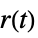 and
and 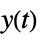 to
to 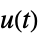
"ClosedLoop" transfer function from 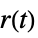 ,
, 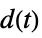 and
and 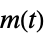 to
to 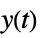
- Properties related to further analysis and simulation:
-
"BlockDiagram" block diagram of csys {"BlockDiagram",<|"SampledData"True|>} create a sampled data block diagram of csys {"ClosedLoop",cspec} detailed control over the form of the closed-loop system - Possible keys for cspec include:
-
"InputModel" input model in csys "Merge" whether to merge csys "ModelName" name of csys "SamplingPeriod" to create a sampled data csys - Properties related to parametrizations of transfer functions:
-
"FeedbackIdealParameters" {kp,ti,td} in 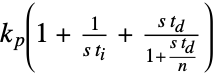
"FeedbackSeriesParameters" {kps,tis,tds} in 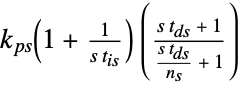
"FeedbackParallelParameters" {kpp,kip,kdp} in 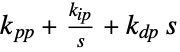
"FeedforwardParameters" {b,c} in the gff 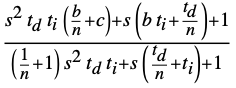
"DerivativeFilterParameter" n controlling derivative filters in gff and gfb - The derivative filter replaces the direct derivative
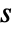 with its filtered version
with its filtered version 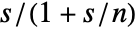 , effectively series connecting a lowpass filter with the derivative.
, effectively series connecting a lowpass filter with the derivative. - Properties related to tuning rule and internal tuning model for sys:
-
"TuningRule" chosen tuning rule "TuningModel" model and parameters {"tmodel",{par1,…}} - The possible tuning models and parameters:
-
{"FOPTD2",{kv,l}} first order plus time delay 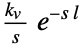
{"FOPTD3",{ks,l,tc} first order plus time delay 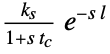
{"Frequency2",{ku,tu}} ultimate gain and ultimate period {"Frequency3",{ku,tu,ks} ultimate gain, ultimate period, and static gain {"SOPTD",{ks,l,tc1,tc2}} second-order plus time delay 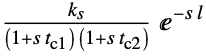
- The parameters are static gain
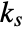 , velocity constant
, velocity constant 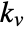 , delay
, delay 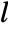 , time constants
, time constants 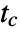 , ultimate gain
, ultimate gain 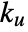 and ultimate period
and ultimate period 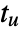 .
. - The following options can be given:
-
PIDFeedforward None reference weights for gff PIDDerivativeFilter None filtered derivative Method Automatic methods to use - The settings for Method control the parameter estimation method used to derive the tuning models.
- Possible settings for Method include:
-
Automatic automatically choose the estimation method "CharacteristicArea" use the characteristic area of the step response "GainMargins" use the phase crossover frequency and gain margin "InflectionPoint" use the inflection point of the step response "MethodOfMoments" match moments "TwoPointSampling" use the 28% and 63% points of the step response
Examples
open all close allBasic Examples (2)
Scope (18)
Basic Uses (4)
Find a PI controller for a plant in state space form:
Or for the plant as a transfer function:
Specify the type of controller:
Proportional integral and derivative:
Evaluate the performance of the resulting controller:
Get the PID parameters in different standard forms suitable for different implementation technologies:
Properties (6)
Obtain the SystemsModelControllerData object and extract a property from it:
Find the computed controllers, PID feedback controller, and feedforward filter:
The feedback controller transfer function and the PID controller:
By default, there is no feedforward filter:
Find closed loop transfer functions from reference, process disturbance, and sensor noise to output:
The reference to output transfer function measures the ability to follow reference changes:
The disturbance to output transfer function measures the ability to reject process disturbances:
The sensor noise to output transfer function measures the ability to reject measurement noise:
The transfer function of the closed-loop system:
The block diagram of the closed-loop system:
Find transfer functions from reference, process disturbance, and sensor noise to control output:
The reference to control transfer function measures the control effort to follow reference:
The disturbance to output transfer function measures the control effort to reject the disturbance:
The sensor noise to output transfer function measures the control effort to reject sensor noise:
Controller Architectures (4)
By default, the controller architecture is a proportional integrating controller:
Specify the controller architecture:
Proportional ("P") controller:
Proportional integral ("PI") controller:
Proportional derivative ("PD") controller:
Proportional integral derivative ("PID") controller:
Filtered PD ("PFD") controller:
Filtered PID ("PIFD") controller:
Use integral action to eliminate steady-state reference following error:
Derivative action may result in a faster reference response:
Tuning Rules (4)
The tuning rule is automatically determined:
The property "TuningRule" gives the tuning rule that was used:
Obtain the automatically selected tuning rule for a given lsys and "carch":
The "CohenCoon" tuning rule allows for PD and PFD architectures:
Controllers designed with the "LoopShaping" rule result in a maximum sensitivity of about 1.4:
The Nyquist plot of the open-loop transfer function lies outside the sensitivity circle of radius 1/1.4:
Options (4)
PIDFeedforward (2)
The default feedforward transfer function is unity:
This may result in a large overshoot to step reference inputs:
Use the PIDFeedforward option to improve the tracking performance:
Automatically compute the reference weights for the feedforward filter:
PIDDerivativeFilter (1)
Applications (3)
Process Control (2)
For a system with three cascaded water tanks, find a PID controller for a constant water level in tank 3:
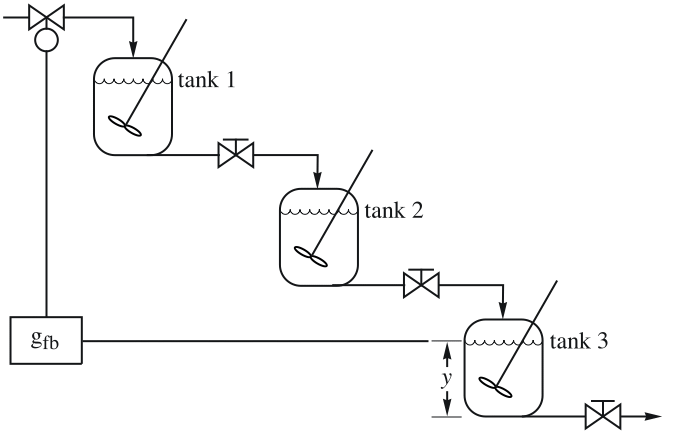
The transfer function from the feed rate in tank 1 to the liquid level in tank 3:
Compute a liquid-level PID controller for the system:
The reference response from the input to the first tank to the water level in the third tank:
The PID controller also improves the gain and phase margins:
An isothermal continuously stirred tank reactor (CSTR):
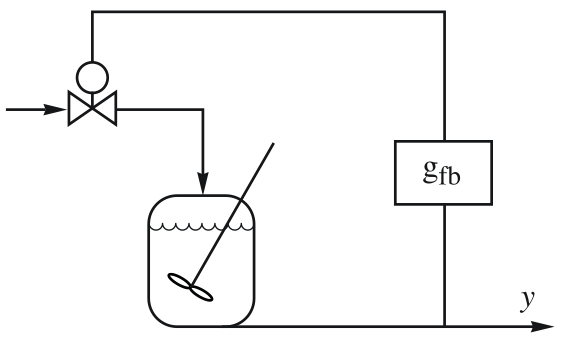
The transfer function from the dilution rate to the product concentration:
Compute a PID controller that controls the product concentration:
The control effort for a set-point change of 0.1 gmol/liter in the product concentration:
The achieved product concentration:
Use a tuning rule, which gives a faster response:
A faster response is accompanied by an increased peak control effort:
Electrical Motor Control (1)
Properties & Relations (2)
Related Guides
Text
Wolfram Research (2012), PIDTune, Wolfram Language function, https://reference.wolfram.com/language/ref/PIDTune.html (updated 2021).
CMS
Wolfram Language. 2012. "PIDTune." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/PIDTune.html.
APA
Wolfram Language. (2012). PIDTune. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PIDTune.html
BibTeX
@misc{reference.wolfram_2025_pidtune, author="Wolfram Research", title="{PIDTune}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/PIDTune.html}", note=[Accessed: 08-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_pidtune, organization={Wolfram Research}, title={PIDTune}, year={2021}, url={https://reference.wolfram.com/language/ref/PIDTune.html}, note=[Accessed: 08-March-2026]}