BUILT-IN MATHEMATICA SYMBOL

PolyLog

gives the polylogarithm function

.

PolyLog

gives the Nielsen generalized polylogarithm function

.

MORE INFORMATION

Mathematical function, suitable for both symbolic and numerical manipulation.

.

.

.

PolyLog has a branch cut discontinuity in the complex 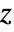plane running from 1 to .

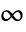For certain special arguments, PolyLog automatically evaluates to exact values.

PolyLog can be evaluated to arbitrary numerical precision.

PolyLog automatically threads over lists.

Out[1]=

Out[1]=

Out[1]=

Scope (7)

Simple exact values are generated automatically:

Evaluate with large order and argument:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Evaluate for complex order and arguments:

PolyLog threads element-wise over lists:

TraditionalForm formatting:

Generalizations & Extensions (7)

Infinite arguments give symbolic results:

PolyLog can be applied to power series:

Evaluate derivatives exactly:

Series expansion at branch cuts:

Series expansion at infinity:

Give the result for an arbitrary symbolic direction:

Special cases:

Series expansion:

Applications (4)

Plot of the absolute value of the dilogarithm function in the complex plane:

Calculate integrals over Fermi-Dirac distributions:

Volume of a hyperbolic dodecahedron with vertices 0, 1,

,

(subject to

):

Plot the volume as a function of the vertex

:

Mahler measure of the trivariate polynomial

as a function of

:

Plot the Mahler measure:

Properties & Relations (6)

Use FullSimplify to simplify polylogarithms:

Use FunctionExpand to expand polylogarithms:

Numerically find a root of a transcendental equation:

Integration:

Generate from integrals and sums:

PolyLog appears in special cases of various mathematical functions:

Possible Issues (1)

Large orders can give results too large to be computed explicitly: