RootLocusPlot[lsys,{k,kmin,kmax}]
generates a root locus plot of a linear time-invariant system lsys as the parameter k ranges from kmin to kmax.




RootLocusPlot
RootLocusPlot[lsys,{k,kmin,kmax}]
generates a root locus plot of a linear time-invariant system lsys as the parameter k ranges from kmin to kmax.
Details and Options



- RootLocusPlot plots the location of poles for the closed-loop system for a range of k values.
- RootLocusPlot treats the parameter k as local, effectively using Block.
- The systems model lsys can be a StateSpaceModel or a TransferFunctionModel.
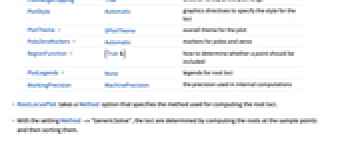
- RootLocusPlot has the same options as Graphics, with the following additions and changes: [List of all options]
-
Axes True whether to draw axes ColorFunction Automatic how to apply coloring to the loci ColorFunctionScaling True whether to scale arguments to ColorFunction EvaluationMonitor None expression to evaluate at every parameter evaluation Exclusions Automatic parameter values to exclude ExclusionsStyle None what to draw at excluded points FeedbackType "Negative" feedback type MaxRecursion Automatic the maximum number of recursive subdivisions allowed Mesh Automatic how many mesh divisions to draw MeshFunctions Automatic how to determine the placement of the mesh divisions MeshShading None how to shade regions between mesh points MeshStyle None the style for mesh divisions Method Automatic the method to determine the loci PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotPoints Automatic initial number of sample parameter points PlotRange Automatic range of values to include PlotRangeClipping True whether to clip at the plot range PlotStyle Automatic graphics directives to specify the style for the loci PlotTheme $PlotTheme overall theme for the plot PoleZeroMarkers Automatic markers for poles and zeros RegionFunction (True&) how to determine whether a point should be included PlotLegends None legends for root loci WorkingPrecision MachinePrecision the precision used in internal computations - RootLocusPlot takes a Method option that specifies the method used for computing the root loci.
- With the setting Method->"GenericSolve", the loci are determined by computing the roots at the sample points and then sorting them.
- With Method->"NDSolve", RootLocusPlot uses NDSolve to solve the differential equation
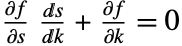 , where
, where 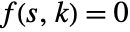 is the characteristic equation of the closed-loop system and
is the characteristic equation of the closed-loop system and 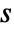 is the complex variable.
is the complex variable. - Method->{"NDSolve",opt1->val1,opt2->val2,…} uses the specified NDSolve options.
- The closed-loop poles for specific values of k can be plotted with appropriate settings for Mesh, MeshFunctions, and MeshStyle.
- ColorData["DefaultPlotColors"] gives the default sequence of colors used by PlotStyle.
- Markers for open-loop poles and zeros, as well as closed-loop poles, can be specified by setting the PoleZeroMarkers option.
- The arguments to RegionFunction are x, y, and k.
-
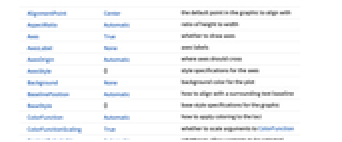
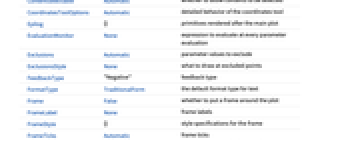
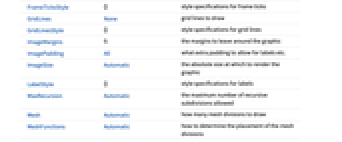
AlignmentPoint Center the default point in the graphic to align with AspectRatio Automatic ratio of height to width Axes True whether to draw axes AxesLabel None axes labels AxesOrigin Automatic where axes should cross AxesStyle {} style specifications for the axes Background None background color for the plot BaselinePosition Automatic how to align with a surrounding text baseline BaseStyle {} base style specifications for the graphic ColorFunction Automatic how to apply coloring to the loci ColorFunctionScaling True whether to scale arguments to ColorFunction ContentSelectable Automatic whether to allow contents to be selected CoordinatesToolOptions Automatic detailed behavior of the coordinates tool Epilog {} primitives rendered after the main plot EvaluationMonitor None expression to evaluate at every parameter evaluation Exclusions Automatic parameter values to exclude ExclusionsStyle None what to draw at excluded points FeedbackType "Negative" feedback type FormatType TraditionalForm the default format type for text Frame False whether to put a frame around the plot FrameLabel None frame labels FrameStyle {} style specifications for the frame FrameTicks Automatic frame ticks FrameTicksStyle {} style specifications for frame ticks GridLines None grid lines to draw GridLinesStyle {} style specifications for grid lines ImageMargins 0. the margins to leave around the graphic ImagePadding All what extra padding to allow for labels etc. ImageSize Automatic the absolute size at which to render the graphic LabelStyle {} style specifications for labels MaxRecursion Automatic the maximum number of recursive subdivisions allowed Mesh Automatic how many mesh divisions to draw MeshFunctions Automatic how to determine the placement of the mesh divisions MeshShading None how to shade regions between mesh points MeshStyle None the style for mesh divisions Method Automatic the method to determine the loci PerformanceGoal $PerformanceGoal aspects of performance to try to optimize PlotLabel None an overall label for the plot PlotLegends None legends for root loci PlotPoints Automatic initial number of sample parameter points PlotRange Automatic range of values to include PlotRangeClipping True whether to clip at the plot range PlotRangePadding Automatic how much to pad the range of values PlotRegion Automatic the final display region to be filled PlotStyle Automatic graphics directives to specify the style for the loci PlotTheme $PlotTheme overall theme for the plot PoleZeroMarkers Automatic markers for poles and zeros PreserveImageOptions Automatic whether to preserve image options when displaying new versions of the same graphic Prolog {} primitives rendered before the main plot RegionFunction (True&) how to determine whether a point should be included RotateLabel True whether to rotate y labels on the frame Ticks Automatic axes ticks TicksStyle {} style specifications for axes ticks WorkingPrecision MachinePrecision the precision used in internal computations
List of all options

Examples
open all close allScope (3)
The root locus plot for various pole-zero configurations:
Root locus plot of a TransferFunctionModel:
Root locus plot of a StateSpaceModel:
Generalizations & Extensions (1)
Options (43)
AspectRatio (4)
By default, the ratio of the height to width for the plot is determined automatically:
Make the height the same as the width with AspectRatio1:
Use numerical values to specify the height-to-width ratio:
AspectRatioFull adjusts the height and width to tightly fit inside other constructs:
Axes (3)
AxesOrigin (2)
AxesStyle (3)
ColorFunction (1)
Epilog (3)
FeedbackType (3)
ImageSize (7)
Use named sizes, such as Tiny, Small, Medium and Large:
Specify the width of the plot:
Specify the height of the plot:
Allow the width and height to be up to a certain size:
Specify the width and height for a graphic, padding with space if necessary:
Setting AspectRatioFull will fill the available space:
Use maximum sizes for the width and height:
Use ImageSizeFull to fill the available space in an object:
Specify the image size as a fraction of the available space:
PlotLegends (4)
Use placeholder legends for root loci:
Use LineLegend to add a overall legend label:
PoleZeroMarkers (6)
Applications (3)
Properties & Relations (6)
The root-locus consists of points with ![]() for negative feedback:
for negative feedback:
And points with ![]() for positive feedback:
for positive feedback:
The root locus plot does not depend on the sampling period:
For strictly proper systems, the root loci go to infinity with straight-line asymptotes:
For the strictly proper system, the number of poles is greater than the number of zeros:
The plot shows four loci going to infinity:
The slopes of the asymptotes for a negative feedback system:
Find where the asymptotes intercept the real axis:
Plot the root loci and the asymptotes:
The slopes of the asymptotes for a positive feedback system:
Plot the root loci and the asymptotes:
The break-away and break-in points on the real axis can be computed from the poles and zeros:
Select those points for which k∈Interval[{0,5}]:
Show the points on the root locus plot:
With the loci and closed-loop poles removed, it becomes a pole-zero plot of the open-loop system:
Use ListPlot to show the same pole-zero plot:
The complex-valued transfer function is a surface with "peaks" at the poles and "valleys" at the zeros:
The root locus plot travels from the "peaks" to the "valleys" along the lines of steepest descent:
The Bode magnitude plot is the intersection of the surface and the ![]() -
-![]() plane:
plane:
See Also
Related Guides
History
Introduced in 2010 (8.0) | Updated in 2012 (9.0) ▪ 2014 (10.0)
Text
Wolfram Research (2010), RootLocusPlot, Wolfram Language function, https://reference.wolfram.com/language/ref/RootLocusPlot.html (updated 2014).
CMS
Wolfram Language. 2010. "RootLocusPlot." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/RootLocusPlot.html.
APA
Wolfram Language. (2010). RootLocusPlot. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/RootLocusPlot.html
BibTeX
@misc{reference.wolfram_2025_rootlocusplot, author="Wolfram Research", title="{RootLocusPlot}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/RootLocusPlot.html}", note=[Accessed: 07-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_rootlocusplot, organization={Wolfram Research}, title={RootLocusPlot}, year={2014}, url={https://reference.wolfram.com/language/ref/RootLocusPlot.html}, note=[Accessed: 07-March-2026]}
