WOLFRAM

Wolfram Language & System Documentation Center
Wolfram Language Home Page »

SpearmanRho
✖
SpearmanRho

✖
SpearmanRho[v1,v2]

gives Spearman's rank correlation coefficient for the vectors v1 and v2.

✖

gives Spearman's rank correlation coefficient for the matrix m.

✖
SpearmanRho[m1,m2]

gives Spearman's rank correlation coefficient for the matrices m1 and m2.

✖
SpearmanRho[dist]

gives Spearman's rank correlation matrix for the multivariate symbolic distribution dist.

✖
SpearmanRho[dist,i,j]

gives the ^(th) Spearman rank correlation for the multivariate symbolic distribution dist.

Details

  • SpearmanRho[v1,v2] gives Spearman's rank correlation coefficient 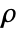between v1 and v2.
  • Spearman's 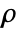is a measure of association based on the rank differences between two lists which indicates how well a monotonic function describes their relationship.
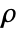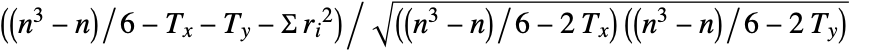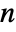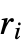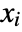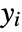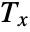  • Spearman's is given by , where is equal to Length[xlist], r_(i) is the rank difference between and , is the correction term for ties in v1, and 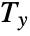is the correction term for ties in v2.
  • SpearmanRho[{v11,v12,…},{v21,v22,…}] is equivalent to Correlation[{r11,r12,…},{r21,r22,…}] where rij is the tie-corrected ranking corresponding to vij.
  • The arguments v1 and v2 can be any real‐valued vectors of equal length.
  • For a matrix m with 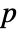columns SpearmanRho[m] is a 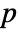× 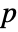matrix of the rank correlations between columns of m.
  • For an 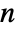× 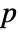matrix m1 and an 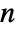× 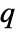matrix m2 SpearmanRho[m1,m2] is a 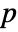× 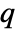matrix of the rank correlations between columns of m1 and columns of m2.
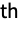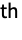  • SpearmanRho[dist,i,j] is 12 Expectation[F[x]G[y],{x,y}disti,j]-3 where F[x] and G[y] are the CDFs of the i^(th) and j^(th) marginals of dist, respectively, and disti,j is the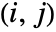 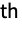^(th) marginal of dist.
  • SpearmanRho[dist] gives a matrix 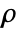where the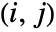 ^(th) entry is given by SpearmanRho[dist,i,j].

Examples

open allclose all

Basic Examples  (4)Summary of the most common use cases

Spearman's for two vectors:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-gugb6d
In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-fulot0
Out[3]=3

Spearman's for a matrix:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-9un6t
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-hz9gv1

Spearman's for two matrices:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-bv14aj
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-ce2wv
In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-i51zwj

Compute Spearman's for a bivariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-f7dh9d
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-mzz2lg

Compare to a simulated value:

In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-nwpxl1

Scope  (7)Survey of the scope of standard use cases

Data  (4)

Exact input yields exact output:

In[4]:=4
✖
https://wolfram.com/xid/0bnhhrimqr19m-kcmch9
Out[4]=4

Approximate input yields approximate output:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-bxeync
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-04fgr
Out[2]=2

Works with large arrays:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-kt50m4
Out[1]=1

SparseArray data can be used:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-h2htud

Distributions and Processes  (3)

Spearman's for a continuous multivariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-fnv00k
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-tekwa
Out[2]=2

Spearman's for derived distributions:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-c3a9y
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-cy97of
In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-etkwz

Data distribution:

In[4]:=4
✖
https://wolfram.com/xid/0bnhhrimqr19m-hxjash
In[5]:=5
✖
https://wolfram.com/xid/0bnhhrimqr19m-gm1a47
In[6]:=6
✖
https://wolfram.com/xid/0bnhhrimqr19m-edj4ah

Spearman's for a random process at times s and t:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-hv1ygl

Applications  (4)Sample problems that can be solved with this function

Spearman's is typically used to detect linear dependence between two vectors:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-l7u46j

The absolute magnitude of tends to 1 given strong linear dependence:

In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-patcg
Out[3]=3

The value tends to 0 for linearly independent vectors:

In[4]:=4
✖
https://wolfram.com/xid/0bnhhrimqr19m-dx1jig
Out[4]=4

Spearman's can be used to measure linear association:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-bcl86
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-g1rlnp
Out[2]=2

Spearman's can only detect monotonic relationships:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-7nvfr
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-nazb6e
In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-j9qi3
In[4]:=4
✖
https://wolfram.com/xid/0bnhhrimqr19m-gtfa0z
Out[4]=4

HoeffdingD can be used to detect a variety of dependence structures:

In[5]:=5
✖
https://wolfram.com/xid/0bnhhrimqr19m-jor85u
Out[5]=5

A collection of measurements were taken from a representative sample of new cars in 1993. Because some of the variables are measured at an ordinal scale, Spearman's is more appropriate than Correlation for measuring monotonic association:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-drd2ab
Out[1]=1
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-gp8q9i
In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-fshejd

A scatter plot matrix of the various metrics:

In[4]:=4
✖
https://wolfram.com/xid/0bnhhrimqr19m-m0cf8q
Out[4]=4

Spearman's corresponding to the scatter plot matrix:

In[5]:=5
✖
https://wolfram.com/xid/0bnhhrimqr19m-cp0h5h

SpearmanRankTest suggests that vehicles with higher horsepower are more costly:

In[6]:=6
✖
https://wolfram.com/xid/0bnhhrimqr19m-bgy446
Out[6]=6

Higher fuel economy meant lower prices in 1993:

In[7]:=7
✖
https://wolfram.com/xid/0bnhhrimqr19m-bh8d2b
Out[7]=7

Properties & Relations  (10)Properties of the function, and connections to other functions

Spearman's ranges from -1 to 1 for high negative and high positive association, respectively:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-fvojjd
In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-cp90d4
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0bnhhrimqr19m-mp4oro
Out[4]=4

Spearman's is Correlation applied to ranks:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-gyy786
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-i1g8cy
Out[2]=2

With no ties, ranks can be computed using ordering:

In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-pyvmky
In[4]:=4
✖
https://wolfram.com/xid/0bnhhrimqr19m-bljs6q
Out[4]=4

Spearman's matrix is symmetric:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-31bc2
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-mmzf9d
Out[2]=2

The diagonal elements of Spearman's matrix are 1:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-o1vsb7
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-h7qlge
Out[2]=2

Spearman's is related to KendallTau:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-hbkym

KendallTau tends to be about of given weak linear association:

In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-mts4te
Out[2]=2

Spearman's will attain 1 or -1 if the variables are perfectly monotonically related:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-xln2s
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-dde2tx
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-gm71p
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0bnhhrimqr19m-kylhyv
Out[4]=4

This is in contrast to Correlation, which strictly measures linear association:

In[5]:=5
✖
https://wolfram.com/xid/0bnhhrimqr19m-f40mz2
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0bnhhrimqr19m-m22vt
Out[6]=6

Spearman's is less sensitive to outliers than Correlation:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-in32zp
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-bfgq4m
Out[2]=2

With outliers:

In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-hn8j42
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0bnhhrimqr19m-jgtad1
Out[4]=4

Without outliers:

In[5]:=5
✖
https://wolfram.com/xid/0bnhhrimqr19m-bbfovu
Out[5]=5
In[6]:=6
✖
https://wolfram.com/xid/0bnhhrimqr19m-ipvl9m
Out[6]=6

Use SpearmanRankTest to test for independence:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-l4v2w
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-eetjj
Out[2]=2

Alternatively, use IndependenceTest to automatically select an appropriate test:

In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-kv172
Out[3]=3

Use CorrelationTest to test a particular value of Spearman's :

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-tkukp

Test against a value of :

In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-be53he
Out[2]=2

Spearman's for a continuous bivariate distribution:

In[1]:=1
✖
https://wolfram.com/xid/0bnhhrimqr19m-bfewud
In[2]:=2
✖
https://wolfram.com/xid/0bnhhrimqr19m-ewdode
Out[2]=2
In[3]:=3
✖
https://wolfram.com/xid/0bnhhrimqr19m-ba93xz
Out[3]=3
In[4]:=4
✖
https://wolfram.com/xid/0bnhhrimqr19m-hqcqde
Out[4]=4
Wolfram Research (2012), SpearmanRho, Wolfram Language function, https://reference.wolfram.com/language/ref/SpearmanRho.html.
✖
Wolfram Research (2012), SpearmanRho, Wolfram Language function, https://reference.wolfram.com/language/ref/SpearmanRho.html.

Text

Wolfram Research (2012), SpearmanRho, Wolfram Language function, https://reference.wolfram.com/language/ref/SpearmanRho.html.

✖
Wolfram Research (2012), SpearmanRho, Wolfram Language function, https://reference.wolfram.com/language/ref/SpearmanRho.html.

CMS

Wolfram Language. 2012. "SpearmanRho." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SpearmanRho.html.

✖
Wolfram Language. 2012. "SpearmanRho." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SpearmanRho.html.

APA

Wolfram Language. (2012). SpearmanRho. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SpearmanRho.html

✖
Wolfram Language. (2012). SpearmanRho. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SpearmanRho.html

BibTeX

@misc{reference.wolfram_2025_spearmanrho, author="Wolfram Research", title="{SpearmanRho}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/SpearmanRho.html}", note=[Accessed: 30-March-2025 ]}

✖
@misc{reference.wolfram_2025_spearmanrho, author="Wolfram Research", title="{SpearmanRho}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/SpearmanRho.html}", note=[Accessed: 30-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_spearmanrho, organization={Wolfram Research}, title={SpearmanRho}, year={2012}, url={https://reference.wolfram.com/language/ref/SpearmanRho.html}, note=[Accessed: 30-March-2025 ]}

✖
@online{reference.wolfram_2025_spearmanrho, organization={Wolfram Research}, title={SpearmanRho}, year={2012}, url={https://reference.wolfram.com/language/ref/SpearmanRho.html}, note=[Accessed: 30-March-2025 ]}