WaveletFilterCoefficients

WaveletFilterCoefficients[wave,filt]

gives the filter coefficients for the symbolic wavelet wave of type filt.

Details and Options

  • WaveletFilterCoefficients[wave,filt] gives a list of the form {{n,cn},{n+1,cn+1},…}, where n is the index and cn the corresponding filter coefficient.
  • For orthogonal wavelets possible filters filt include: "PrimalLowpass" and "PrimalHighpass".
  • The primal highpass filter coefficients satisfy 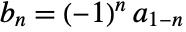, where 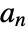are primal lowpass filter coefficients.
  • The scaling function 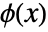and wavelet function 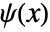satisfy the relations:
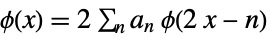
  • (primal) scaling refinement equation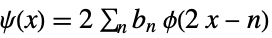
    (primal) wavelet refinement equation
  • For biorthogonal wavelets, possible filters filt include: "PrimalLowpass", "PrimalHighpass", "DualLowpass", and "DualHighpass".
  • The primal highpass filter coefficients satisfy 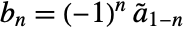, where 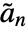are dual lowpass filter coefficients. Dual highpass filter coefficients satisfy 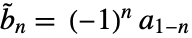, where 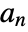are primal lowpass filter coefficients.
  • The primal scaling function 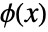and wavelet function 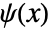satisfy the relations:
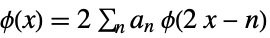
  • (primal) scaling refinement equation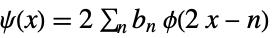
    (primal) wavelet refinement equation
  • The dual scaling function 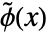and dual wavelet function 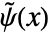satisfy:
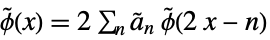
  • (dual) scaling refinement equation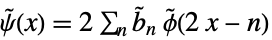
    (dual) wavelet refinement equation
  • For discrete wavelets with compact support, you can also produce LiftingFilterData objects used for LiftingWaveletTransform as well as generating compiled standalone wavelet transform code. The following filt values can be used:
  • "LiftingFilter"default lifting filter
    "AllLiftingFilter"all possible lifting filters
    "BestLiftingFilter"most stable lifting filter
  • With the option setting WorkingPrecision->prec, filter coefficients are computed using precision prec. By default, WorkingPrecision->MachinePrecision is used.

Examples

open allclose all

Basic Examples  (4)

Primal lowpass filter coefficients:

Primal highpass filter coefficients:

Dual lowpass filter coefficients:

Dual highpass filter coefficients:

Scope  (5)

Compute primal lowpass filter coefficients:

Primal highpass filter coefficients:

Dual lowpass filter coefficients:

Dual highpass filter coefficients:

"Properties" gives a list of available properties:

Properties for BiorthogonalSplineWavelet:

Options  (2)

WorkingPrecision  (2)

By default WorkingPrecision->MachinePrecision is used:

Use higher-precision filter computation:

Properties & Relations  (3)

Lowpass filter coefficients sum to unity; :

Highpass filter coefficients sum to zero; :

The lowpass and highpass filter coefficients are orthogonal; :

Wolfram Research (2010), WaveletFilterCoefficients, Wolfram Language function, https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html.

Text

Wolfram Research (2010), WaveletFilterCoefficients, Wolfram Language function, https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html.

CMS

Wolfram Language. 2010. "WaveletFilterCoefficients." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html.

APA

Wolfram Language. (2010). WaveletFilterCoefficients. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html

BibTeX

@misc{reference.wolfram_2025_waveletfiltercoefficients, author="Wolfram Research", title="{WaveletFilterCoefficients}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html}", note=[Accessed: 13-March-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_waveletfiltercoefficients, organization={Wolfram Research}, title={WaveletFilterCoefficients}, year={2010}, url={https://reference.wolfram.com/language/ref/WaveletFilterCoefficients.html}, note=[Accessed: 13-March-2025 ]}