BUILT-IN MATHEMATICA SYMBOL

WaveletThreshold

WaveletThreshold[dwd]
thresholds the detail wavelet coefficients in the DiscreteWaveletData object dwd.

WaveletThreshold[dwd, tspec]
thresholds the coefficients using the thresholding specification tspec.

WaveletThreshold[dwd, tspec, wind]
thresholds the wavelet coefficients given by the wavelet indices wind.

Details Details

WaveletThreshold[dwd] is effectively WaveletThreshold[dwd, "Universal"].
WaveletThreshold[dwd, tspec, wind] indicates which wavelet coefficients to threshold, using the same index convention as described for DiscreteWaveletData.
By default, thresholding is performed on detail coefficients at each refinement level.
The threshold specification tspec can be of the form: tfun, .
Possible tfun names and options include:

	{"Hard",}
	{"Soft",}
	{"Firm",,r,p}
	{"PiecewiseGarrote",}	$0 TemplateBox[{x}, Abs]<=delta; x-(delta^2)/x TemplateBox[{x}, Abs]>delta$
	{"SmoothGarrote",,n}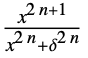
	{"Hyperbola",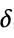}	$ 0 TemplateBox[{x}, Abs]<=delta; sgn(x) sqrt(x^2-delta^2) TemplateBox[{x}, Abs]>delta;$
	{"LargestCoefficients",k}	keep the largest k coefficients

In all cases 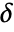is assumed to be a positive number or a thresholding function tfunc to compute 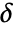. Each should return a positive number.
The parameter conditions for are that 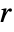is a positive real and 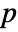a positive real number between 0 and 1.
The parameter conditions for are to have 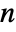be a positive real number.
The threshold 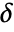can be automatically computed using the following methods:

	Automatic	thresholding value
	{"FDR",}	false discovery rate at significance level
	"GCV"	minimizes generalized cross-validation function
	"GCVLevel"	performed at each level
	"SURE"	Stein's unbiased risk estimate
	"SUREHybrid"	combination of and thresholding
	"SURELevel"	performed at each level
	"Universal"	Donoho and Johnstone's universal threshold
	"UniversalLevel"	performed at each level