WilksW
WilksW[m1,m2]
gives Wilks's for the matrices m1 and m2.
Details
- WilksW[m1,m2] gives Wilks's between m1 and m2.
- Wilks's is a measure of linear dependence based on partitions of the pooled covariance matrix.
- Wilks's is computed as
![1-TemplateBox[{Sigma}, Det]/(TemplateBox[{{Sigma, _, {(, 11, )}}}, Det] TemplateBox[{{Sigma, _, {(, 22, )}}}, Det])](Files/WilksW.en/1.png "1-TemplateBox[{Sigma}, Det]/(TemplateBox[{{Sigma, _, {(, 11, )}}}, Det] TemplateBox[{{Sigma, _, {(, 22, )}}}, Det])")
where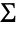 
is the covariance matrix of the pooled sample which can be partitioned into 
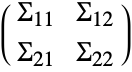, where 
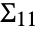and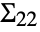 
correspond to the covariance matrices of the individual datasets. - The arguments m1 and m2 can be any real‐valued matrices or vectors of equal length.
Examples
open all close allBasic Examples (3)
Scope (3)
Properties & Relations (3)
Wilks's measures linear dependence:
Wilks's cannot detect nonlinear dependency:
HoeffdingD can be used to detect some nonlinear dependence structures:
The statistical significance of can be tested using WilksWTest:
Alternatively, use IndependenceTest to automatically choose a test:
Text
Wolfram Research (2012), WilksW, Wolfram Language function, https://reference.wolfram.com/language/ref/WilksW.html.
CMS
Wolfram Language. 2012. "WilksW." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/WilksW.html.
APA
Wolfram Language. (2012). WilksW. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/WilksW.html