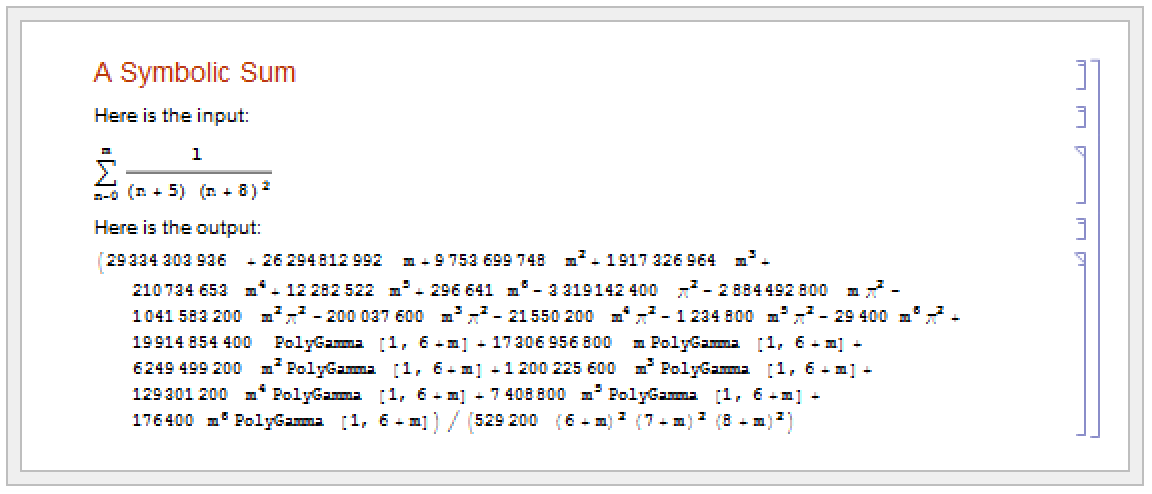
Input and Output in Notebooks
Input and Output in Notebooks
click on α | use a button in a palette |
| \[Alpha] | use a full name |
| EscaEsc or EscalphaEsc |
use a standard alias (shown below as
Esc
a
Esc
)
|
| Esc\alphaEsc | use a TeX alias |
| EscαEsc | use an HTML alias |
Enter common Greek letters with a palette. Open it with the Palettes ▶ Special Characters menu item:
Note that in the Wolfram Language the letter  stands for Pi. None of the other Greek letters have special meanings.
stands for Pi. None of the other Greek letters have special meanings.
In a notebook, you can also give the two‐dimensional input xy directly. The Wolfram Language again interprets this as a power:
One way to enter a two‐dimensional form such as xy into a Wolfram System notebook is to paste this form into the notebook by clicking the appropriate button in the palette.
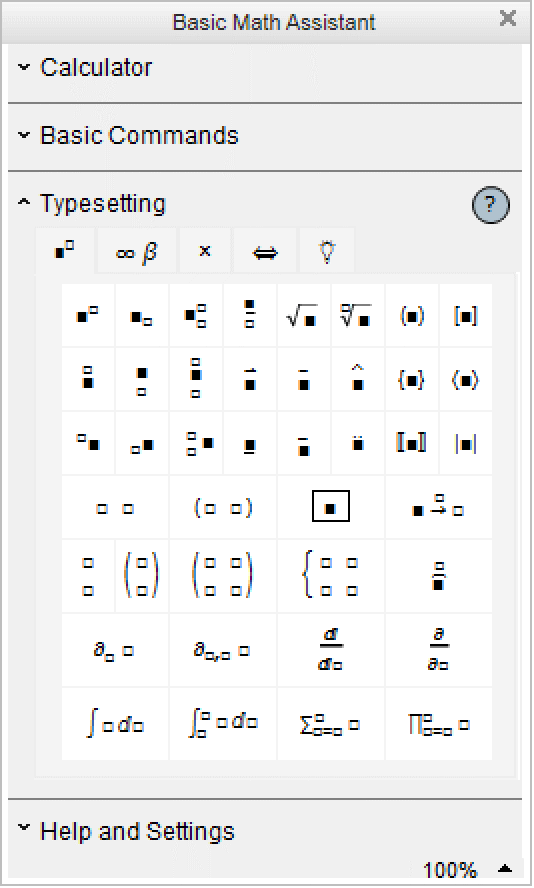
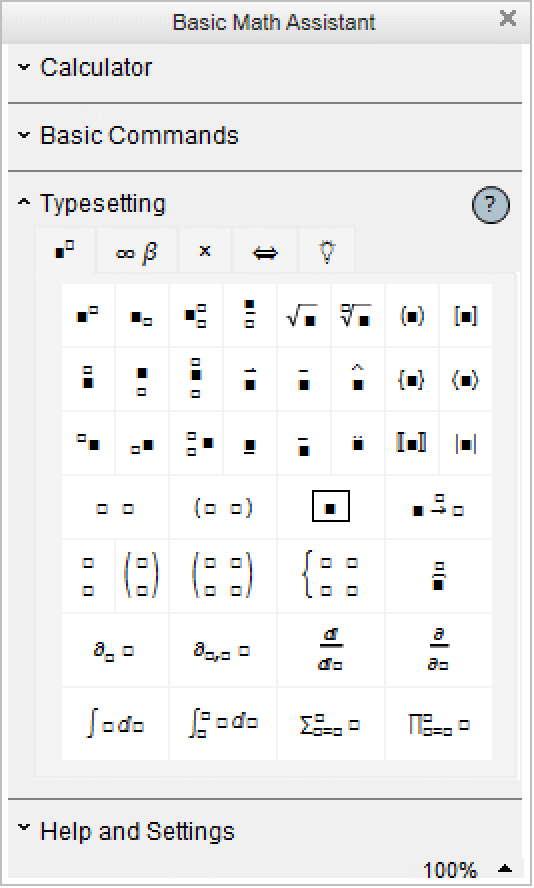
The Palettes ▶ Basic Math Assistant palette can be used to enter common two‐dimensional math notations.
x Ctrl+^ y Ctrl+Space | use control keys that exist on most keyboards |
x Ctrl+6 y Ctrl+Space | use control keys that should exist on all keyboards |
You type Ctrl+^ by holding down the Control key, then pressing the ^ key. As soon as you do this, your cursor will jump to a superscript position. You can then type anything you want and it will appear in that position.
When you have finished, press Ctrl+Space to move back down from the superscript position. You type Ctrl+Space by holding down the Control key, then pressing the Space bar.
You can remember the fact that Ctrl+^ gives you a superscript by thinking of Ctrl+^ as just a more immediate form of ^. When you type x^y, the Wolfram Language will leave this one‐dimensional form unchanged until you explicitly process it. But if you type x Ctrl+^ y then the Wolfram Language will immediately give you a superscript.
On a standard English‐language keyboard, the character ^ appears as the shifted version of 6. The Wolfram Language therefore accepts Ctrl+6 as an alternative to Ctrl+^. Note that if you are using something other than a standard English‐language keyboard, the Wolfram Language will almost always accept Ctrl+6 but may not accept Ctrl+^.
x Ctrl+_ y Ctrl+Space | use control keys that exist on most keyboards |
x Ctrl+- y Ctrl+Space | use control keys that should exist on all keyboards |
Subscripts in the Wolfram Language work very much like superscripts. However, whereas the Wolfram Language automatically interprets xy as x raised to the power y, it has no similar interpretation for xy. Instead, it just treats xy as a purely symbolic object.
But pressing Ctrl+Space takes you out of the denominator, so the +z does not appear in the denominator:
Ctrl+@ x Ctrl+Space | use control keys that exist on most keyboards |
Ctrl+2 x Ctrl+Space | use control keys that should exist on all keyboards |
Ctrl+^ or Ctrl+6 | go to the superscript position |
Ctrl+_ or Ctrl+- | go to the subscript position |
Ctrl+@ or Ctrl+2 | go into a square root |
Ctrl+% or Ctrl+5 |
go from subscript to superscript or vice versa, or to the exponent position in a root
|
Ctrl
+
/
| go to the denominator for a fraction |
Ctrl
+
Space
| return from a special position |
Special input forms based on control characters. The second forms given should work on any keyboard.
In addition to subscripts and superscripts, the Wolfram Language also supports the notion of underscripts and overscripts—elements that go directly underneath or above. Among other things, you can use underscripts and overscripts to enter the limits of sums and products.
x Ctrl+Shift+, y Ctrl+Space | |
create an underscript | |
x Ctrl+& y Ctrl+Space or x Ctrl+7 y Ctrl+Space | |
create an overscript | |
When you see a two‐dimensional expression on the screen, you can edit it much as you would edit text. You can for example place your cursor somewhere and start typing. Or you can select a part of the expression, then remove it using the Delete key, or insert a new version by typing it in.
In addition to ordinary text editing features, there are some keys that you can use to move around in two‐dimensional expressions.
Ctrl
+
.
| select the next larger subexpression |
Ctrl
+
Space
| move to the right of the current structure |
→
| move to the next character |
←
| move to the previous character |
Shift
+
Enter
| evaluate the whole current cell |
Shift
+
Ctrl
+
Enter
(Windows/Unix/Linux) or
Cmd
+
Return
(Mac OS X)
| |
evaluate only the selected subexpression | |
In most computations, you will want to go from one step to the next by taking the whole expression that you have generated, and then evaluating it. But if for example you are trying to manipulate a single formula to put it into a particular form, you may instead find it more convenient to perform a sequence of operations separately on different parts of the expression.
You do this by selecting each part you want to operate on, then inserting the operation you want to perform, then using Shift+Ctrl+Enter for Windows/Unix/Linux or Cmd+Return for Mac OS X.
Pressing Shift+Ctrl+Enter (Windows/Unix/Linux) or Cmd+Return (Mac OS X) evaluates the selected part.
The Basic Commands ▶ y=x tab in the Basic Math Assistant, Classroom Assistant, and Writing Assistant palettes also provides a number of convenient operations which will transform in place any selected subexpression.
character | short form | long form | symbol |
| EscpEsc | \[Pi] | Pi | |
| EscinfEsc | \[Infinity] | Infinity | |
| EscdegEsc | \[Degree] | Degree |
special characters | short form | long form | ordinary characters |
| x≤y | x Esc<=Esc y | x \[LessEqual] y | x <= y |
| x≥y | x Esc>=Esc y | x \[GreaterEqual] y | x >= y |
| x≠y | x Esc!=Esc y | x \[NotEqual] y | x != y |
| x∈y | x EscelEsc y | x \[Element] y | Element[x,y] |
| xy | x Esc->Esc y | x \[Rule] y | x -> y |
Special forms for a few operators. "Operator Input Forms" gives a complete list.
When you type the ordinary-character form for certain operators, the front end automatically replaces them with the special-character form. For instance, when you type the last three examples, the front end automatically substitutes the  character for ->.
character for ->.
special characters | short form | long form | ordinary characters |
| x ÷ y | x EscdivEsc y | x \[Divide] y | x / y |
| x × y | x Esc*Esc y | x \[Times] y | x * y |
| x y | x EsccrossEsc y | x \[Cross] y | Cross[x,y] |
| x y | x Esc==Esc y | x \[Equal] y | x == y |
| x y | x Escl=Esc y | x \[LongEqual] y | x == y |
| x ∧ y | x Esc&&Esc y | x \[And] y | x && y |
| x ∨ y | x Esc||Esc y | x \[Or] y | x || y |
| ¬ x | Esc!Esc x | \[Not] x | ! x |
| x y | x Esc=>Esc y | x \[Implies] y | x => y |
| x ⋃ y | x EscunEsc y | x \[Union] y | Union[x,y] |
| x ⋂ y | x EscinterEsc y | x \[Intersection] y | Intersection[x,y] |
| x y | x Esc,Esc y | x \[InvisibleComma] y | x , y |
| f x | f Esc@Esc x | f \[InvisibleApplication] x | f @ x or f[x] |
| x | x Esc+Esc | x \[ImplicitPlus] | x + y / z |
Many of the forms of input discussed here use special characters, but otherwise just consist of ordinary one‐dimensional lines of text. Wolfram System notebooks, however, also make it possible to use two‐dimensional forms of input.
two-dimensional | one-dimensional | |
| x^y | power | |
| x/y | division | |
| Sqrt[x] | square root | |
| x^(1/n) | ||
| Sum[f,{i,imin,imax}] | sum | |
| Product[f,{i,imin,imax}] | product | |
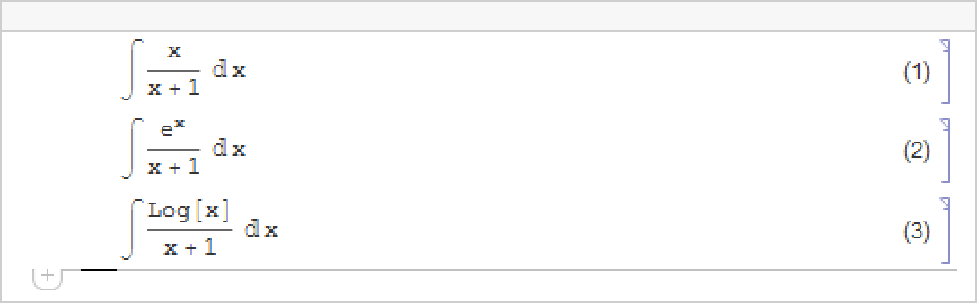
| Integrate[f,x] | indefinite integral | |
| Integrate[f,{x,xmin,xmax}] | definite integral | |
| D[f,x] | partial derivative | |
| D[f,x,y] | multivariate partial derivative | |
| Conjugate[x] | complex conjugate | |
| Transpose[m] | transpose | |
| ConjugateTranspose[m] | conjugate transpose | |
| Part[expr,i,j,…] | part extraction |
You can enter two‐dimensional forms using any of the mechanisms discussed in "Entering Two-Dimensional Input". Note that upper and lower limits for sums and products must be entered as overscripts and underscripts—not superscripts and subscripts.
short form | long form | |
| EscsumEsc | \[Sum] | summation sign |
| EscprodEsc | \[Product] | product sign |
| EscintEsc | \[Integral] | integral sign |
| EscddEsc | \[DifferentialD] | special |
| EscpdEsc | \[PartialD] | partial derivative operator |
| EsccoEsc | \[Conjugate] | conjugate symbol |
| EsctrEsc | \[Transpose] | transpose symbol |
| EscctEsc | \[ConjugateTranspose] | conjugate transpose symbol |
| Esc[[Esc | \[LeftDoubleBracket] | part brackets |
Some special characters used in entering formulas. "Mathematical and Other Notation" gives a complete list.
You should realize that even though a summation sign can look almost identical to a capital sigma it is treated in a very different way by the Wolfram Language. The point is that a sigma is just a letter; but a summation sign is an operator which tells the Wolfram Language to perform a Sum operation.
Much as the Wolfram Language distinguishes between a summation sign and a capital sigma, it also distinguishes between an ordinary d, the "partial d" ∂ that is used for taking derivatives, and the special "differential d" 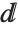 that is used in the standard notation for integrals. It is crucial that you use the differential
that is used in the standard notation for integrals. It is crucial that you use the differential 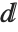 —entered as EscddEsc—when you type in an integral. If you try to use an ordinary d, the Wolfram Language will just interpret this as a symbol called d—it will not understand that you are entering the second part of an integration operator.
—entered as EscddEsc—when you type in an integral. If you try to use an ordinary d, the Wolfram Language will just interpret this as a symbol called d—it will not understand that you are entering the second part of an integration operator.
The Wolfram System front end provides an Insert ▶ Table/Matrix submenu for creating and editing arrays with any specified number of rows and columns. Once you have such an array, you can edit it to fill in whatever elements you want.
Putting parentheses around the array makes it look more like a matrix, but does not affect its interpretation:
Ctrl
+
,
| add a column |
Ctrl
+
Enter
| add a row |
Tab
| go to the next or element |
Ctrl
+
Space
| move out of the table or matrix |
Note that you can use Ctrl+, and Ctrl+Enter to start building up an array, and particularly for small arrays this is often more convenient than using the New menu item in the Table/Matrix submenu. The Table/Matrix menu items typically allow you to make basic adjustments, such as drawing lines between rows or columns.
Entering a Piecewise expression is a special case of entering a table.
You can make an element in a table span over multiple rows or columns by selecting the entire block that you want the element to span and using the Insert ▶ Table/Matrix ▶ Make Spanning menu command. To split a spanning element into individual components, use Insert ▶ Table/Matrix ▶ Split Spanning.
Unless you specifically tell it otherwise, the Wolfram System will interpret a superscript as a power:
Ctrl+_ or Ctrl+- | go to the position for a subscript |
Ctrl
+
Shift
+
,
| go to the position underneath |
Ctrl+^ or Ctrl+6 | go to the position for a superscript |
Ctrl+& or Ctrl+7 | go to the position on top |
Ctrl
+
Space
| return from a special position |
Special input forms based on control characters. The second forms given should work on any keyboard.
Just as Ctrl+^ and Ctrl+_ go to superscript and subscript positions, so also Ctrl+& and Ctrl+4 can be used to go to positions directly above and below. With the layout of a standard English‐language keyboard Ctrl+& is directly to the right of Ctrl+^ while Ctrl+4 is directly to the right of Ctrl+_.
key sequence | displayed form | expression form |
x Ctrl+& _ | OverBar[x] | |
x Ctrl+& EscvecEsc | OverVector[x] | |
x Ctrl+& ~ | OverTilde[x] | |
x Ctrl+& ^ | OverHat[x] | |
x Ctrl+& . | OverDot[x] | |
x Ctrl+Shift+, _ | UnderBar[x] |
If you enter text in languages other than English, you will typically need to use various additional accented and other characters. If your computer system is set up in an appropriate way, then you will be able to enter such characters directly using standard keys on your keyboard. But however your system is set up, the Wolfram Language always provides a uniform way to handle such characters.
|
|
You should realize that there is no uniform standard for computer keyboards around the world, and as a result it is inevitable that some details of what has been said in this tutorial may not apply to your keyboard.
In particular, the identification for example of Ctrl+6 with Ctrl+^ is valid only for keyboards on which ^ appears as Shift+6. On other keyboards, the Wolfram System uses Ctrl+6 to go to a superscript position, but not necessarily Ctrl+^.
Regardless of how your keyboard is set up you can always use palettes or menu items to set up superscripts and other kinds of notation. And assuming you have some way to enter characters such as ∖, you can always give input using full names such as \[Infinity].
The Wolfram Language supports an extremely wide range of mathematical notation, although often it does not assign a predefined meaning to it. Thus, for example, you can enter an expression such as x⊕y, but the Wolfram Language will not initially make any assumption about what you mean by  .
.
The Wolfram Language knows that  is an operator, but it does not initially assign any specific meaning to it:
is an operator, but it does not initially assign any specific meaning to it:
There are some forms which look like characters on a standard keyboard, but which are interpreted in a different way by the Wolfram Language. Thus, for example, ∖[Backslash] or Esc displays as ∖ but is not interpreted in the same way as a ∖ typed directly on the keyboard.
displays as ∖ but is not interpreted in the same way as a ∖ typed directly on the keyboard.
Most operators work like  and go in between their operands. But some operators can go in other places. Thus, for example, Esc
and go in between their operands. But some operators can go in other places. Thus, for example, Esc and Esc
and Esc or ∖[LeftAngleBracket] and ∖[RightAngleBracket] are effectively operators which go around their operand.
or ∖[LeftAngleBracket] and ∖[RightAngleBracket] are effectively operators which go around their operand.
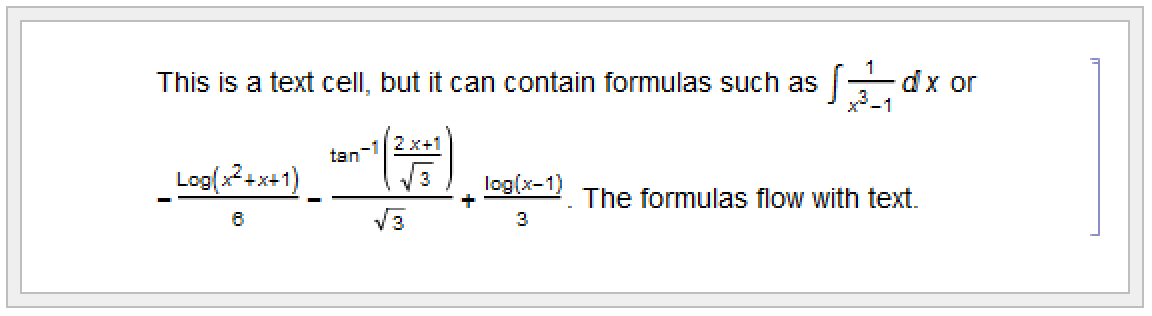
The simplest way to mix text and formulas in a Wolfram System notebook is to put each kind of material in a separate cell. Sometimes, however, you may want to embed a formula within a cell of text, or vice versa.
Ctrl+( or Ctrl+9 |
begin entering a formula within text, or text within a formula
|
Ctrl+) or Ctrl+0 |
end entering a formula within text, or text within a formula
|
Wolfram System notebooks often contain both formulas that are intended for actual evaluation by the Wolfram Language, and ones that are intended just to be read in a more passive way.
When you insert a formula in text, you can use the Convert to StandardForm and Convert to TraditionalForm menu items within the formula to convert it to StandardForm or TraditionalForm. StandardForm is normally appropriate whenever the formula is thought of as a Wolfram System program fragment.
In general, however, you can use exactly the same mechanisms for entering formulas, whether or not they will ultimately be given as Wolfram Language input.
You should realize, however, that to make the detailed typography of typical formulas look as good as possible, the Wolfram Language automatically does things such as inserting spaces around certain operators. But these kinds of adjustments can potentially be inappropriate if you use notation in very different ways from the ones the Wolfram Language is expecting. In such cases, you may have to make detailed typographical adjustments by hand.
Depending on the purpose for which you are using a Wolfram System notebook, you may want to change its overall appearance. The front end allows you to specify independently the styles to be used for display on the screen and for printing. Typically you can do this by choosing appropriate items in the Format menu.
| ScreenStyleEnvironment | styles to be used for screen display |
| PrintingStyleEnvironment | styles to be used for printed output |
| Working | standard style definitions for screen display |
| Presentation | style definitions for presentations |
| SlideShow | style definitions for displaying presentation slides |
| Printout | style definitions for printed output |
menu item to make the selected object a hyperlink | |
| Hyperlink["uri"] | generate as output a hyperlink with the label and destination set as uri |
| Hyperlink["label","uri"] | generate as output a hyperlink with the label label and the destination uri |
| Hyperlink[{"file.nb",None}] | generate as output a hyperlink to the specified notebook |
| Hyperlink[{"file.nb","tag"}] | generate as output a hyperlink to the cell tagged as tag in the specified notebook |
A hyperlink is a special kind of button which jumps to another part of a notebook when it is pressed. Typically hyperlinks are indicated in the Wolfram System by blue text.
To set up a hyperlink, just select the text or other object that you want to be a hyperlink. Then choose the menu item Insert ▶ Hyperlink and fill in the specification of where you want the destination of the hyperlink to be.
The destination of a hyperlink can be any standard web address (URI). Hyperlinks can also point to notebooks on the local file system, or even to specific cells inside those notebooks. Hyperlinks which point to specific cells in notebooks use cell tags to identify the cells. If a particular cell tag is used for more than one cell in a given notebook, then the hyperlink will go to the first instance of a cell with that cell tag.
A hyperlink can be generated in output by using the Wolfram Language command Hyperlink. These hyperlinks can be copied and pasted into text or used in a larger interface being generated by the Wolfram Language.
Using the DisplayFormulaNumbered Style
These cells are in DisplayFormulaNumbered style. DisplayFormulaNumbered style is available in the default stylesheet.
Using the AutomaticNumbering Menu Item
The input for each cell here is exactly the same, but the cells contain an element that displays as a progressively larger number as one goes through the notebook.
Wolfram System notebooks provide the basic technology that you need to be able to create a very wide range of sophisticated interactive documents. But to get the best out of this technology you need to develop an appropriate style of exposition.
Many people at first tend to use Wolfram System notebooks either as simple worksheets containing a sequence of input and output lines, or as onscreen versions of traditional books and other printed material. But the most effective and productive uses of Wolfram System notebooks tend to lie at neither one of these extremes, and instead typically involve a fine‐grained mixing of Wolfram Language input and output with explanatory text. In most cases the single most important factor in obtaining such fine‐grained mixing is uniform use of the Wolfram Language.
One might think that there would tend to be four kinds of material in a Wolfram System notebook: plain text, mathematical formulas, computer code, and interactive interfaces. But one of the key ideas of the Wolfram Language is to provide a single language that offers the best of both traditional mathematical formulas and computer code.
In StandardForm, Wolfram Language expressions have the same kind of compactness and elegance as traditional mathematical formulas. But unlike such formulas, Wolfram Language expressions are set up in a completely consistent and uniform way. As a result, if you use Wolfram Language expressions, then regardless of your subject matter, you never have to go back and reexplain your basic notation: it is always just the notation of the Wolfram Language. In addition, if you set up your explanations in terms of Wolfram Language expressions, then a reader of your notebook can immediately take what you have given, and actually execute it as Wolfram Language input.
If one has spent many years working with traditional mathematical notation, then it takes a little time to get used to seeing mathematical facts presented as StandardForm Wolfram Language expressions. Indeed, at first one often has a tendency to try to use TraditionalForm whenever possible, perhaps with hidden tags to indicate its interpretation. But quite soon one tends to evolve to a mixture of StandardForm and TraditionalForm. And in the end it becomes clear that StandardForm alone is for most purposes the most effective form of presentation.
In traditional mathematical exposition, there are many tricks for replacing chunks of text by fragments of formulas. In StandardForm many of these same tricks can be used. But the fact that Wolfram Language expressions can represent not only mathematical objects but also procedures, algorithms, graphics, and interfaces increases greatly the extent to which chunks of text can be replaced by shorter and more precise material.
The Wolfram System provides systemwide support for a large number of special characters. Each character has a name and a number of shortcut aliases. They are fully supported by the standard Wolfram System fonts.
Interpretation of Characters
The interpretations given here are those used in StandardForm and InputForm. Most of the interpretations also work in TraditionalForm.
You can override the interpretations by giving your own rules for MakeExpression.
Letters and letter‐like forms | used in symbol names |
Infix operators | e.g. |
Prefix operators | e.g. |
Postfix operators | e.g. |
Matchfix operators | e.g. |
Compound operators | e.g. |
Raw operators | operator characters that can be typed on an ordinary keyboard |
Spacing characters | interpreted in the same way as an ordinary space |
Structural elements | characters used to specify structure; usually ignored in interpretation |
Uninterpretable elements | characters indicating missing information |
Infix operators for which no grouping is specified in the listing are interpreted so that for example 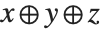 becomes CirclePlus[x,y,z].
becomes CirclePlus[x,y,z].
Naming Conventions
Characters that correspond to built‐in Wolfram Language functions typically have names corresponding to those functions. Other characters typically have names that are as generic as possible.
| \[Capital…] | uppercase form of a letter |
| \[Left…] and \[Right…] |
pieces of a matchfix operator (also arrows)
|
| \[Raw…] | a printable ASCII character |
| \[…Indicator] | a visual representation of a keyboard character |
style |
Script
,
Gothic
, etc.
|
variation | |
case |
Capital
, etc.
|
modifiers | |
direction | |
base | |
diacritical mark |
Acute
,
Ring
, etc.
|
Aliases
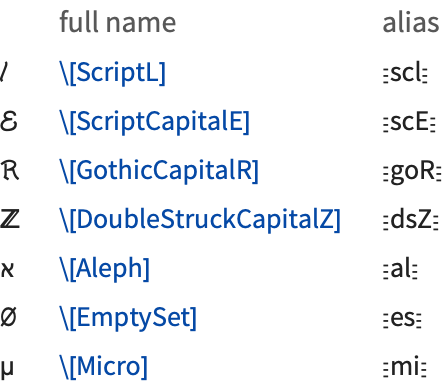
The Wolfram Language supports both its own system of aliases, as well as aliases based on character names in TeX and SGML or HTML. Except where they conflict, character names corresponding to plain TeX, LaTeX and AMSTeX are all supported. Note that TeX and SGML or HTML aliases are not given explicitly in the list of characters below.
- Characters that are alternatives to standard keyboard operators use these operators as their aliases (e.g. Esc->Esc for
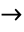 , Esc&&Esc for
, Esc&&Esc for 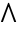 ).
). - Most single‐letter aliases stand for Greek letters.
- Capital‐letter characters have aliases beginning with capital letters.
- When there is ambiguity in the assignment of aliases, a space is inserted at the beginning of the alias for the less common character (e.g. Esc->Esc for \[Rule] and Esc␣->Esc for \[RightArrow]).
- ! is inserted at the beginning of the alias for a Not character.
- TeX aliases begin with a backslash ∖.
- SGML aliases begin with an ampersand &.
- User‐defined aliases conventionally begin with a dot or comma.
Font Matching
The special fonts provided with the Wolfram System include all the characters given in this listing. Some of these characters also appear in certain ordinary text fonts.