Numerical Operations on Functions
Numerical Operations on Functions
Spaces denote multiplication in the Wolfram Language. The front end automatically replaces spaces between numbers with light gray multiplication signs:
Arithmetic operations in the Wolfram Language are grouped according to the standard mathematical conventions. As usual, 2^3+4, for example, means (2^3)+4, and not 2^(3+4). You can always control grouping by explicitly using parentheses.
With the Wolfram Language, you can perform calculations with a particular precision, usually higher than an ordinary calculator. When given precise numbers, the Wolfram Language does not convert them to an approximate representation, but gives a precise result.
One of the important features of the Wolfram Language is its ability to give you exact, symbolic results for computations. There are, however, computations where it is just mathematically impossible to get exact "closed form" results. In such cases, you can still often get approximate numerical results.
When the Wolfram Language cannot find an explicit result for something like a definite integral, it returns a symbolic form. You can take this symbolic form and try to get an approximate numerical value by applying N.
By giving a second argument to N, you can specify the numerical precision to use:
If you want to evaluate an integral numerically in the Wolfram Language, then using Integrate and applying N to the result is not the most efficient way to do it. It is better instead to use the function NIntegrate, which immediately gives a numerical answer, without first trying to get an exact symbolic result. You should realize that even when Integrate does not in the end manage to give you an exact result, it may spend a lot of time trying to do so.
NIntegrate evaluates numerical integrals directly, without first trying to get a symbolic result:
| Integrate | NIntegrate | definite integrals |
| Sum | NSum | sums |
| Product | NProduct | products |
| Solve | NSolve | solutions of algebraic equations |
| DSolve | NDSolve | solutions of differential equations |
| Maximize | NMaximize | maximization |
The Wolfram System does operations like numerical integration very differently from the way it does their symbolic counterparts.
When you do a symbolic integral, the Wolfram System takes the functional form of the integrand you have given, and applies a sequence of exact symbolic transformation rules to it, to try and evaluate the integral.
However, when the Wolfram System does a numerical integral, after some initial symbolic preprocessing, the only information it has about your integrand is a sequence of numerical values for it. To get a definite result for the integral, the Wolfram System then effectively has to make certain assumptions about the smoothness and other properties of your integrand. If you give a sufficiently pathological integrand, these assumptions may not be valid, and as a result, the Wolfram System may simply give you the wrong answer for the integral.
This problem may occur, for example, if you try to integrate numerically a function which has a very thin spike at a particular position. The Wolfram System samples your function at a number of points, and then assumes that the function varies smoothly between these points. As a result, if none of the sample points come close to the spike, then the spike will go undetected, and its contribution to the numerical integral will not be correctly included.
If, however, you ask for the integral from 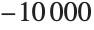 to
to 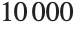 , with its default settings NIntegrate will miss the peak near
, with its default settings NIntegrate will miss the peak near  , and give the wrong answer:
, and give the wrong answer:
NIntegrate tries to make the best possible use of the information that it can get about the numerical values of the integrand. Thus, for example, by default, if NIntegrate notices that the estimated error in the integral in a particular region is large, it will take more samples in that region. In this way, NIntegrate tries to "adapt" its operation to the particular integrand you have given.
The kind of adaptive procedure that NIntegrate uses is similar, at least in spirit, to what Plot does in trying to draw smooth curves for functions. In both cases, the Wolfram System tries to go on taking more samples in a particular region until it has effectively found a smooth approximation to the function in that region.
The kinds of problems that can appear in numerical integration can also arise in doing other numerical operations on functions.
For example, if you ask for a numerical approximation to the sum of an infinite series, the Wolfram System samples a certain number of terms in the series, and then does an extrapolation to estimate the contributions of other terms. If you insert large terms far out in the series, they may not be detected when the extrapolation is done, and the result you get for the sum may be incorrect.
A similar problem arises when you try to find a numerical approximation to the minimum of a function. The Wolfram System samples only a finite number of values, then effectively assumes that the actual function interpolates smoothly between these values. If in fact the function has a sharp dip in a particular region, then the Wolfram System may miss this dip, and you may get the wrong answer for the minimum.
If you work only with numerical values of functions, there is simply no way to avoid the kinds of problems discussed here. Exact symbolic computation, of course, allows you to get around these problems.
In many calculations, it is therefore worthwhile to go as far as you can symbolically, and then resort to numerical methods only at the very end. This gives you the best chance of avoiding the problems that can arise in purely numerical computations.
| NSum[f,{i,imin,Infinity}] | numerical approximation to |
| NProduct[f,{i,imin,Infinity}] | numerical approximation to |
| NIntegrate[f,{x,xmin,xmax}] | numerical approximation to |
| NIntegrate[f,{x,xmin,xmax},{y,ymin,ymax}] | |
the multiple integral | |
NIntegrate can handle singularities in the integration region:
Here is a double integral over a triangular domain. Note the order in which the variables are given:
| N[Integrate[expr,{x,xmin,xmax}]] |
try to perform an integral exactly, then find numerical approximations to the parts that remain
|
| NIntegrate[expr,{x,xmin,xmax}] | find a numerical approximation to an integral |
| NIntegrate[expr,{x,xmin,xmax},{y,ymin,ymax},…] | |
multidimensional numerical integral | |
| NIntegrate[expr,{x,xmin,x1,x2,…,xmax}] | |
do a numerical integral along a line, starting at
| |
An important feature of NIntegrate is its ability to deal with functions that "blow up" at known points. NIntegrate automatically checks for such problems at the endpoints of the integration region.
The function 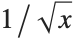 blows up at
blows up at  , but NIntegrate still succeeds in getting the correct value for the integral:
, but NIntegrate still succeeds in getting the correct value for the integral:

NIntegrate automatically looks for singularities at the endpoints of the integration region and any subregions defined by piecewise functions (such as Piecewise and Abs) in the integrand. If additional singularities are present, NIntegrate may not give you the right answer for the integral. Nevertheless, in following its adaptive procedure, NIntegrate will often detect the presence of potentially singular behavior, and will warn you about it.
NIntegrate warns you of a possible problem due to the singularity in the middle of the integration region. The final result is numerically quite close to the correct answer:
If you know that your integrand has singularities at particular points, you can explicitly tell NIntegrate to deal with them. NIntegrate[expr,{x,xmin,x1,x2,…,xmax}] integrates expr from xmin to xmax, looking for possible singularities at each of the intermediate points xi.
You can also use the list of intermediate points xi in NIntegrate to specify an integration contour to follow in the complex plane. The contour is taken to consist of a sequence of line segments, starting at xmin, going through each of the xi, and ending at xmax.
This integrates 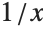 around a closed contour in the complex plane, going from
around a closed contour in the complex plane, going from 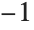 through the points
through the points  ,
,  , and
, and  , then back to
, then back to  :
:
option name | default value | |
| MinRecursion | 0 | minimum number of recursions for the integration method |
| MaxRecursion | Automatic | maximum number of recursions for the integration method |
| MaxPoints | Automatic | maximum total number of times to sample the integrand |
Special options for NIntegrate.
When NIntegrate tries to evaluate a numerical integral, it samples the integrand at a sequence of points. If it finds that the integrand changes rapidly in a particular region, then it recursively takes more sample points in that region. The parameters MinRecursion and MaxRecursion specify the minimum and maximum number of recursions to use. Increasing the value of MinRecursion guarantees that NIntegrate will use a larger number of sample points. MaxPoints and MaxRecursion limit the number of sample points which NIntegrate will ever try to use. Increasing MinRecursion or MaxRecursion will make NIntegrate work more slowly.
With the default settings for all options, NIntegrate misses the peak in  near
near  , and gives the wrong answer for the integral:
, and gives the wrong answer for the integral:
With the option MinRecursion->3, NIntegrate samples enough points that it notices the peak around  . With the default setting of MaxRecursion, however, NIntegrate cannot use enough sample points to be able to expect an accurate answer:
. With the default setting of MaxRecursion, however, NIntegrate cannot use enough sample points to be able to expect an accurate answer:
Another way to solve the problem is to make NIntegrate break the integration region into several pieces, with a small piece that explicitly covers the neighborhood of the peak:
For integrals in many dimensions, it can take a long time for NIntegrate to get a precise answer. However, by setting the option MaxPoints, you can tell NIntegrate to give you just a rough estimate, sampling the integrand only a limited number of times.
| NSum[f,{i,imin,imax}] | find a numerical approximation to the sum |
| NSum[f,{i,imin,imaxdi}] | use step |
| NProduct[f,{i,imin,imax}] | find a numerical approximation to the product |
You can apply N explicitly to get a numerical result:
The way NSum works is to include a certain number of terms explicitly, and then to try and estimate the contribution of the remaining ones. There are three approaches to estimating this contribution. The first uses the Euler–Maclaurin method, and is based on approximating the sum by an integral. The second method, known as the Wynn epsilon method, samples a number of additional terms in the sum, and then tries to fit them to a polynomial multiplied by a decaying exponential. The third approach, useful for alternating series, uses an alternating signs method; it also samples a number of additional terms and approximates their sum by the ratio of two polynomials (Padé approximation).
option name | default value | |
| Method | Automatic | |
| NSumTerms | 15 | number of terms to include explicitly |
| VerifyConvergence | True | whether the convergence of the series should be verified |
Special options for NSum.
If you do not explicitly specify the method to use, NSum will try to choose between the EulerMaclaurin or WynnEpsilon methods. In any case, some implicit assumptions about the functions you are summing have to be made. If these assumptions are not correct, you may get inaccurate answers.
The most common place to use NSum is in evaluating sums with infinite limits. You can, however, also use it for sums with finite limits. By making implicit assumptions about the objects you are evaluating, NSum can often avoid doing as many function evaluations as an explicit Sum computation would require.
You can also get the result, albeit much less efficiently, by constructing the symbolic form of the sum, then evaluating it numerically:
| NSolve[lhs==rhs,x] | solve a polynomial equation numerically |
| NSolve[{lhs1==rhs1,lhs2==rhs2,…},{x,y,…}] | |
solve a system of polynomial equations numerically | |
| FindRoot[lhs==rhs,{x,x0}] |
search for a numerical solution to an equation, starting at
|
| FindRoot[{lhs1==rhs1,lhs2==rhs2,…},{{x,x0},{y,y0},…}] | |
search for numerical solutions to simultaneous equations | |
NSolve gives you numerical approximations to all the roots of a polynomial equation:
You can also use NSolve to solve sets of simultaneous equations numerically:
If your equations involve only linear functions or polynomials, then you can use NSolve to get numerical approximations to all the solutions. However, when your equations involve more complicated functions, there is in general no systematic procedure for finding all solutions, even numerically. In such cases, you can use FindRoot to search for solutions. You have to give FindRoot a place to start its search.
The equation has several solutions. If you start at a different  , FindRoot may return a different solution:
, FindRoot may return a different solution:
When Solve cannot find solutions in terms of radicals to polynomial equations, it returns a symbolic form of the result in terms of Root objects:
You can get numerical solutions by applying N:
You can use NSolve to get numerical solutions to polynomial equations directly, without first trying to find exact results:
| NSolve[poly==0,x] | get approximate numerical solutions to a polynomial equation |
| NSolve[poly==0,x,n] | get solutions using |
| NSolve[{eqn1,eqn2,…},{var1,var2,…}] | |
get solutions to a polynomial system | |
NSolve will give you the complete set of numerical solutions to any polynomial equation or system of polynomial equations.
NSolve can find solutions to sets of simultaneous polynomial equations:
NSolve gives you a general way to find numerical approximations to the solutions of polynomial equations. Finding numerical solutions to more general equations, however, can be much more difficult, as discussed in "Equations in One Variable". FindRoot gives you a way to search for a numerical root of a function or a numerical solution to an arbitrary equation, or set of equations.
| FindRoot[f,{x,x0}] | search for a numerical root of f, starting with x=x0 |
| FindRoot[lhs==rhs,{x,x0}] | search for a numerical solution to the equation lhs==rhs, starting with x=x0 |
| FindRoot[f1,f2,…,{{x,x0},{y,y0},…}] | |
search for a simultaneous numerical root of all the fi | |
| FindRoot[{eqn1,eqn2,…},{{x,x0},{y,y0},…}] | |
search for a numerical solution to the simultaneous equations eqni | |
This finds a numerical approximation to the value of  at which the intersection occurs. The 0 tells FindRoot what value of
at which the intersection occurs. The 0 tells FindRoot what value of  to try first:
to try first:
In trying to find a solution to your equation, FindRoot starts at the point you specify, and then progressively tries to get closer and closer to a solution. Even if your equations have several solutions, FindRoot always returns the first solution it finds. Which solution this is will depend on what starting point you chose. If you start sufficiently close to a particular solution, FindRoot will usually return that solution.
The function  has an infinite number of roots of the form
has an infinite number of roots of the form 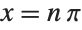 . If you start sufficiently close to a particular root, FindRoot will give you that root:
. If you start sufficiently close to a particular root, FindRoot will give you that root:
If you want FindRoot to search for complex solutions, then you have to give a complex starting value:
The variables used by FindRoot can have values that are lists. This allows you to find roots of functions that take vectors as arguments.
| NDSolve[eqns,y,{x,xmin,xmax}] | solve numerically for the function y, with the independent variable x in the range xmin to xmax |
| NDSolve[eqns,{y1,y2,…},{x,xmin,xmax}] | |
solve a system of equations for the yi | |
This generates a numerical solution to the equation  with
with 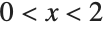 . The result is given in terms of an InterpolatingFunction:
. The result is given in terms of an InterpolatingFunction:
With an algebraic equation such as 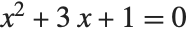 , each solution for
, each solution for 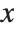 is simply a single number. For a differential equation, however, the solution is a function, rather than a single number. For example, in the equation
is simply a single number. For a differential equation, however, the solution is a function, rather than a single number. For example, in the equation 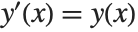 , you want to get an approximation to the function
, you want to get an approximation to the function 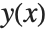 as the independent variable
as the independent variable 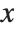 varies over some range.
varies over some range.
The Wolfram Language represents numerical approximations to functions as InterpolatingFunction objects. These objects are functions which, when applied to a particular 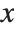 , return the approximate value of
, return the approximate value of 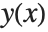 at that point. The InterpolatingFunction effectively stores a table of values for
at that point. The InterpolatingFunction effectively stores a table of values for 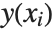 , then interpolates this table to find an approximation to
, then interpolates this table to find an approximation to 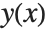 at the particular
at the particular 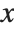 you request.
you request.
| y[x]/.solution | use the list of rules for the function y to get values for y[x] |
| InterpolatingFunction[data][x] | evaluate an interpolated function at the point x |
| Plot[Evaluate[y[x]/.solution],{x,xmin,xmax}] | |
plot the solution to a differential equation | |
Using results from NDSolve.
| NDSolve[eqn,u,{x,xmin,xmax},{t,tmin,tmax},…] | |
solve a partial differential equation | |
The function NDSolve discussed in "Numerical Differential Equations" allows you to find numerical solutions to differential equations. NDSolve handles both single differential equations and sets of simultaneous differential equations. It can handle a wide range of ordinary differential equations as well as some partial differential equations. In a system of ordinary differential equations there can be any number of unknown functions 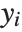 , but all of these functions must depend on a single "independent variable"
, but all of these functions must depend on a single "independent variable" 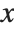 , which is the same for each function. Partial differential equations involve two or more independent variables. NDSolve can also handle differential‐algebraic equations that mix differential equations with algebraic ones.
, which is the same for each function. Partial differential equations involve two or more independent variables. NDSolve can also handle differential‐algebraic equations that mix differential equations with algebraic ones.
| NDSolve[{eqn1,eqn2,…},y,{x,xmin,xmax}] | |
find a numerical solution for the function y with x in the range xmin to xmax | |
| NDSolve[{eqn1,eqn2,…},{y1,y2,…},{x,xmin,xmax}] | |
find numerical solutions for several functions yi | |
NDSolve represents solutions for the functions yi as InterpolatingFunction objects. The InterpolatingFunction objects provide approximations to the yi over the range of values xmin to xmax for the independent variable x.
NDSolve finds solutions iteratively. It starts at a particular value of x, then takes a sequence of steps, trying eventually to cover the whole range xmin to xmax.
In order to get started, NDSolve has to be given appropriate initial or boundary conditions for the yi and their derivatives. These conditions specify values for yi[x], and perhaps derivatives yi'[x], at particular points x. In general, at least for ordinary differential equations, the conditions you give can be at any x: NDSolve will automatically cover the range xmin to xmax.
When you use NDSolve, the initial or boundary conditions you give must be sufficient to determine the solutions for the yi completely. When you use DSolve to find symbolic solutions to differential equations, you can get away with specifying fewer initial conditions. The reason is that DSolve automatically inserts arbitrary constants C[i] to represent degrees of freedom associated with initial conditions that you have not specified explicitly. Since NDSolve must give a numerical solution, it cannot represent these kinds of additional degrees of freedom. As a result, you must explicitly give all the initial or boundary conditions that are needed to determine the solution.
In a typical case, if you have differential equations with up to 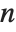 th derivatives, then you need to give initial conditions for up to
th derivatives, then you need to give initial conditions for up to  th derivatives, or give boundary conditions at
th derivatives, or give boundary conditions at 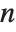 points.
points.
The Wolfram Language allows you to use any appropriate linear combination of function values and derivatives as boundary conditions:
In most cases, all the initial conditions you give must involve the same value of x, say x0. As a result, you can avoid giving both xmin and xmax explicitly. If you specify your range of x as {x,x1}, then the Wolfram Language will automatically generate a solution over the range x0 to x1.
You can give initial conditions as equations of any kind. In some cases, these equations may have multiple solutions. In such cases, NDSolve will correspondingly generate multiple solutions.
You can use NDSolve to solve systems of coupled differential equations.
Unknown functions in differential equations do not necessarily have to be represented by single symbols. If you have a large number of unknown functions, you will often find it more convenient, for example, to give the functions names like y[i].
NDSolve can handle functions whose values are lists or arrays. If you give initial conditions like y[0]=={v1,v2,…,vn}, then NDSolve will assume that y is a function whose values are lists of length n.
option name | default value | |
| MaxSteps | Automatic | maximum number of steps in |
| StartingStepSize | Automatic | starting size of step in |
| MaxStepSize | Automatic | maximum size of step in |
| NormFunction | Automatic | the norm to use for error estimation |
Special options for NDSolve.
NDSolve has many methods for solving equations, but essentially all of them at some level work by taking a sequence of steps in the independent variable 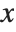 , and using an adaptive procedure to determine the size of these steps. In general, if the solution appears to be varying rapidly in a particular region, then NDSolve will reduce the step size or change the method so as to be able to track the solution better.
, and using an adaptive procedure to determine the size of these steps. In general, if the solution appears to be varying rapidly in a particular region, then NDSolve will reduce the step size or change the method so as to be able to track the solution better.
Through its adaptive procedure, NDSolve is able to solve "stiff" differential equations in which there are several components that vary with 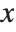 at very different rates.
at very different rates.
NDSolve nevertheless tracks both components successfully:
NDSolve follows the general procedure of reducing step size until it tracks solutions accurately. There is a problem, however, when the true solution has a singularity or the integration interval is too big. For the first case, NDSolve limits the smallest step size that it will consider as significant for a given integration interval. For the second case, the option MaxSteps specifies the maximum number of steps that NDSolve will ever take in attempting to find a solution. For ordinary differential equations the default setting is MaxStepsAutomatic. With the Automatic setting, NDSolve will estimate how many steps are needed to solve the equation at hand based on the initial step sizes taken.
NDSolve stops when the step size becomes too small:
The default setting for MaxSteps should be sufficient for most equations with smooth solutions. When solutions have a complicated structure, however, you may occasionally have to choose larger settings for MaxSteps. With the setting MaxSteps->Infinity, there is no upper limit on the number of steps used.
To take the solution to the Lorenz equations this far, you need to remove the default bound on MaxSteps:
When NDSolve solves a particular set of differential equations, it always tries to choose a step size appropriate for those equations. In some cases, the very first step that NDSolve makes may be too large, and it may miss an important feature in the solution. To avoid this problem, you can explicitly set the option StartingStepSize to specify the size to use for the first step.
The equations you give to NDSolve do not necessarily all have to involve derivatives; they can also just be algebraic. You can use NDSolve to solve many such differential‐algebraic equations.
| NDSolve[{eqn1,eqn2,…},u,{t,tmin,tmax},{x,xmin,xmax},…] | |
solve a system of partial differential equations for u | |
| NDSolve[{eqn1,eqn2,…},{u1,u2,…},{t,tmin,tmax},{x,xmin,xmax},…] | |
solve a system of partial differential equations for several functions ui | |
This finds a numerical solution to the wave equation. The result is a two‐dimensional interpolating function:
| FindMinimum[f,{x,x0}] | search for a local minimum of f, starting at x=x0 |
| FindMinimum[f,x] | search for a local minimum of f |
| FindMinimum[f,{{x,x0},{y,y0},…}] | |
search for a local minimum in several variables | |
| FindMinimum[{f,cons},{{x,x0},{y,y0},…}] | |
search for a local minimum subject to the constraints cons starting at x=x0, y=y0, … | |
| FindMinimum[{f,cons},{x,y,…}] | search for a local minimum subject to the constraints cons |
| FindMaximum[f,x]
, etc.
| search for a local maximum |
Like FindRoot, FindMinimum and FindMaximum work by starting from a point, then progressively searching for a minimum or maximum. But since they return a result as soon as they find anything, they may give only a local minimum or maximum of your function, not a global one.
| NMinimize[f,x] | try to find the global minimum of f |
| NMinimize[f,{x,y,…}] | try to find the global minimum over several variables |
| NMaximize[f,x] | try to find the global maximum of f |
| NMaximize[f,{x,y,…}] | try to find the global maximum over several variables |
NMinimize and NMaximize are numerical analogs of Minimize and Maximize. But unlike Minimize and Maximize they usually cannot guarantee to find absolute global minima and maxima. Nevertheless, they typically work well when the function f is fairly smooth, and has a limited number of local minima and maxima.
| NMinimize[{f,cons},{x,y,…}] | try to find the global minimum of f subject to constraints cons |
| NMaximize[{f,cons},{x,y,…}] | try to find the global maximum of f subject to constraints cons |
In this case Minimize can give an exact result:
This gives a numerical approximation, effectively using NMinimize:
If both the objective function f and the constraints cons are linear in all variables, then minimization and maximization correspond to a linear programming problem. Sometimes it is convenient to state such problems not in terms of explicit equations, but instead in terms of matrices and vectors.
| LinearProgramming[c,m,b] | find the vector |
| LinearProgramming[c,m,b,l] | use the constraints |
You can specify a mixture of equality and inequality constraints by making the list 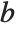 be a sequence of pairs
be a sequence of pairs 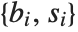 . If
. If 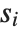 is
is  , then the
, then the 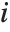 th constraint is
th constraint is 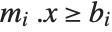 . If
. If 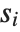 is
is  then it is
then it is 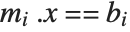 , and if
, and if 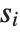 is
is 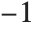 then it is
then it is 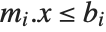 .
.
In LinearProgramming[c,m,b,l], you can make 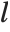 be a list of pairs
be a list of pairs  representing lower and upper bounds on the
representing lower and upper bounds on the 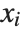 .
.
In doing large linear programming problems, it is often convenient to give the matrix 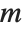 as a SparseArray object.
as a SparseArray object.
In doing numerical operations like NDSolve and NMinimize, the Wolfram Language by default uses machine numbers. But by setting the option WorkingPrecision->n you can tell it to use arbitrary‐precision numbers with n‐digit precision.
When you give a setting for WorkingPrecision, this typically defines an upper limit on the precision of the results from a computation. But within this constraint you can tell the Wolfram Language how much precision and accuracy you want it to try to get. You should realize that for many kinds of numerical operations, increasing precision and accuracy goals by only a few digits can greatly increase the computation time required. Nevertheless, there are many cases where it is important to ensure that high precision and accuracy are obtained.
| WorkingPrecision | the number of digits to use for computations |
| PrecisionGoal | the number of digits of precision to try to get |
| AccuracyGoal | the number of digits of accuracy to try to get |

Given a particular setting for WorkingPrecision, each of the functions for numerical operations in the Wolfram Language uses certain default settings for PrecisionGoal and AccuracyGoal. Typical is the case of NDSolve, in which these default settings are equal to half the settings given for WorkingPrecision.
The precision and accuracy goals normally apply both to the final results returned, and to various norms or error estimates for them. Functions for numerical operations in the Wolfram Language typically try to refine their results until either the specified precision goal or accuracy goal is reached. If the setting for either of these goals is Infinity, then only the other goal is considered.
In doing ordinary numerical evaluation with N[expr,n], the Wolfram Language automatically adjusts its internal computations to achieve n‐digit precision in the result. But in doing numerical operations on functions, it is in practice usually necessary to specify WorkingPrecision and PrecisionGoal more explicitly.
Functions in the Wolfram Language are carefully set up so that you normally do not have to know how they work inside. But particularly for numerical functions that use iterative algorithms, it is sometimes useful to be able to monitor the internal progress of these algorithms.
| StepMonitor | an expression to evaluate whenever a successful step is taken |
| EvaluationMonitor | an expression to evaluate whenever functions from the input are evaluated |
Note the importance of using option:>expr rather than option->expr. You need a delayed rule :> to make expr be evaluated each time it is used, rather than just when the rule is given.
To take a successful step toward an answer, iterative numerical algorithms sometimes have to do several evaluations of the functions they have been given. Sometimes this is because each step requires, say, estimating a derivative from differences between function values, and sometimes it is because several attempts are needed to achieve a successful step.
| Method->Automatic |
pick methods automatically (default)
|
| Method->"name" | specify an explicit method to use |
| Method->{"name",{"par1"->val1,…}} | specify more details of a method |
Method options.
There are often several different methods known for doing particular types of numerical computations. Typically the Wolfram Language supports most generally successful ones that have been discussed in the literature, as well as many that have not. For any specific problem, it goes to considerable effort to pick the best method automatically. But if you have sophisticated knowledge of a problem, or are studying numerical methods for their own sake, you may find it useful to tell the Wolfram Language explicitly what method it should use. Function reference pages list some of the methods built into the Wolfram Language; others are discussed in "Numerical and Related Functions" or in advanced documentation.
This solves a differential equation using method 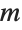 , and returns the number of steps and evaluations needed:
, and returns the number of steps and evaluations needed:
With the method selected automatically, this is the number of steps and evaluations that are needed:
This shows what happens with several other possible methods. The Adams method that is selected automatically is the fastest:
This shows what happens with the explicit Runge–Kutta method when the difference order parameter is changed:
Functions that are specified by simple algebraic formulas tend to be such that when their input is changed only slightly, their output also changes only slightly. But functions that are instead based on executing procedures quite often show almost arbitrarily sensitive dependence on their input. Typically the reason this happens is that the procedure "excavates" progressively less and less significant digits in the input.
Here is the result with input 0.1112. Progressive divergence from the result with input 0.1111 is seen:
The action of FractionalPart[2x] is particularly simple in terms of the binary digits of the number x: it just drops the first one, and shifts the remaining ones to the left. After several steps, this means that the results one gets are inevitably sensitive to digits that are far to the right, and have an extremely small effect on the original value of x.
If you give input only to a particular precision, you are effectively specifying only a certain number of digits. And once all these digits have been "excavated" you can no longer get accurate results, since to do so would require knowing more digits of your original input. So long as you use arbitrary‐precision numbers, the Wolfram Language automatically keeps track of this kind of degradation in precision, indicating a number with no remaining significant digits by 0.×10e, as discussed in "Arbitrary-Precision Numbers".
Successive steps yield numbers of progressively lower precision, and eventually no precision at all:
This asks for the precision of each number. Zero precision indicates that there are no correct significant digits:
It is important to realize that if you use approximate numbers of any kind, then in an example like the one above you will always eventually run out of precision. But so long as you use arbitrary‐precision numbers, the Wolfram Language will explicitly show you any decrease in precision that is occurring. However, if you use machine‐precision numbers, then the Wolfram Language will not keep track of precision, and you cannot tell when your results become meaningless.
If you use machine‐precision numbers, the Wolfram Language will no longer keep track of any degradation in precision:
By iterating the operation FractionalPart[2x] you extract successive binary digits in whatever number you start with. And if these digits are apparently random—as in a number like 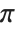 —then the results will be correspondingly random. But if the digits have a simple pattern—as in any rational number—then the results you get will be correspondingly simple.
—then the results will be correspondingly random. But if the digits have a simple pattern—as in any rational number—then the results you get will be correspondingly simple.
By iterating an operation such as FractionalPart[3/2x] it turns out however to be possible to get seemingly random sequences even from very simple input. This is an example of a very general phenomenon first identified by Stephen Wolfram in the mid‐1980s, which has nothing directly to do with sensitive dependence on input.
Many kinds of iterative procedures yield functions that depend sensitively on their input. Such functions also arise when one looks at solutions to differential equations. In effect, varying the independent parameter in the differential equation is a continuous analog of going from one step to the next in an iterative procedure.