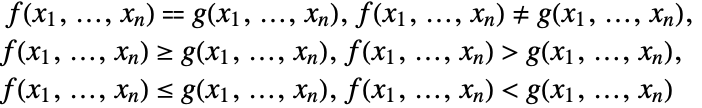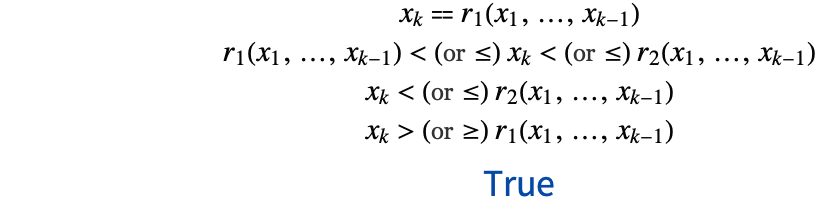Real Polynomial Systems
| Introduction | Arbitrary Real Polynomial Systems |
| Cylindrical Algebraic Decomposition | Options |
| Decision Problems, FindInstance, and Assumptions | References |
Introduction
A real polynomial system is an expression constructed with polynomial equations and inequalities
combined using logical connectives and quantifiers
An occurrence of a variable 
inside 
or 
is called a bound occurrence; any other occurrence of 
is called a free occurrence. A variable 
is called a free variable of a real polynomial system if the system contains a free occurrence of 
. A real polynomial system is quantifier free if it contains no quantifiers.
An example of a real polynomial system with free variables 
, 
, and 
is the following:
Any real polynomial system can be transformed to the prenex normal form
where each 
is 
or 
, and 
is a quantifier-free formula called the quantifier-free part of the system.
Any quantifier-free real polynomial system can be transformed to the disjunctive normal form
where each 
is a polynomial equation or inequality.
Reduce, Resolve, and FindInstance always put real polynomial systems in the prenex normal form, with quantifier-free parts in the disjunctive normal form, and subtract sides of equations and inequalities to put them in the form
In this tutorial, it is always assumed the system has been transformed to this form.
Reduce can solve arbitrary real polynomial systems. For a system with free variables 
, the solution (possibly after expanding 
with respect to 
) is a disjunction of terms of the form
and 
and 
are algebraic functions (expressed using Root objects or radicals) such that for all 
satisfying 
, 
and 
are well defined (that is, denominators and leading terms of Root objects are nonzero), real valued, continuous, and satisfy inequality 
.
The subset of 
described by formula (4) is called a cell. The cells described by different terms of solution of a real polynomial system are disjoint.
Resolve can eliminate quantifiers from arbitrary real polynomial systems. If no variables are specified in the input and all input polynomials are at most quadratic in the bound variables, Resolve may be able to eliminate the quantifiers without solving the resulting system. Otherwise, Resolve uses the same algorithm and gives the same answer as Reduce.
FindInstance can handle arbitrary real polynomial systems, giving instances of real solutions or an empty list for systems that have no solutions. If the number of instances requested is more than one, the instances are randomly generated from the full solution of the system and therefore may depend on the value of the RandomSeed option. If one instance is requested and the system does not contain general (
) quantifiers, a faster algorithm producing one instance is used and the instance returned is always the same.
The main general tool used in solving real polynomial systems is the Cylindrical Algebraic Decomposition (CAD) algorithm (see, for example, [1]). CAD for real polynomial systems is available in the Wolfram Language directly as CylindricalDecomposition. There are also several other algorithms used to solve special case problems.
Cylindrical Algebraic Decomposition
Semialgebraic Sets and Cell Decomposition
A subset of 
is semialgebraic if it is a solution set of a quantifier-free real polynomial system. According to Tarski's theorem [2], solution sets of arbitrary (quantified) real polynomial systems are semialgebraic.
Every semialgebraic set can be represented as a finite union of disjoint cells [3] defined recursively as follows:
- A cell in
is a point or an open interval - A cell in
has one of the two forms
where 
is a cell in 
, 
is a continuous algebraic function, 
and 
are continuous algebraic functions, or 
or 
, and 
on 
.
By an algebraic function we mean a function 
for which there is a polynomial
In the Wolfram Language algebraic functions can be represented as Root objects or radicals.
The CAD algorithm, introduced by Collins [4], computes a cell decomposition of solution sets of arbitrary real polynomial systems. The objective of the original Collins algorithm was to eliminate quantifiers from a quantified real polynomial system and to produce an equivalent quantifier-free polynomial system. After finding a cell decomposition, the algorithm performed an additional step of finding an implicit representation of the semialgebraic set in terms of polynomial equations and inequalities in the free variables. The objective of Reduce is somewhat different. Given a semialgebraic set presented by a real polynomial system, quantified or not, Reduce finds a cell decomposition of the set, explicitly written in terms of algebraic functions.
While Reduce may use other methods to solve the system, CylindricalDecomposition gives a direct access to the CAD algorithm. For a real polynomial system, CylindricalDecomposition gives a nested formula representing disjunction of cells in the solved form (4). As in the output of Reduce, the cells are disjoint and additionally are always ordered lexicographically with respect to ranges of the subsequent variables.
SemialgebraicComponentInstances gives at least one sample point in each connected component of a semialgebraic set. The function uses the CAD algorithm and returns a sample point in each of the constructed cells.
The Projection Phase of the CAD Algorithm
Finding a cell decomposition of a semialgebraic set using the CAD algorithm consists of two phases, projection and lifting. In the projection phase, we start with the set 
of factors of the polynomials present in the quantifier-free part 
of the system (2) and eliminate variables one by one using a projection operator 
such that
Generally speaking, if all polynomials of 
have constant signs on a cell 
, then all polynomials of 
are delineable over 
, that is, each has a fixed number of real roots on 
as a polynomial in 
, the roots are continuous functions on 
, they have constant multiplicities, and two roots of two of the polynomials are equal either everywhere or nowhere in 
. Variables are ordered so that
This way the roots of polynomials of 
are the algebraic functions needed in the construction of the cell decomposition of the semialgebraic set.
Several improvements have reduced the size of the original Collins projection. The currently best projection operator applicable in all cases is due to Hong [5]; however, in most situations we can use a smaller projection operator given by McCallum [6, 7], with an improvement by Brown [8]. There are even smaller projection operators that can be applied in some special cases. When equational constraints are present, we can use the projection operator suggested by Collins [9], and developed and proven by McCallum [10, 11]. When there are no equations and only strict inequalities, and there are no free variables or we are interested only in the full-dimensional part of the semialgebraic set, we can use an even smaller projection operator described in [12, 13]. For systems containing equational constraints that generate a zero-dimensional ideal, Gröbner bases are used to find projection polynomials.
The Wolfram Language uses the smallest of the previously mentioned projections that is appropriate for the given example. Whenever applicable, we use the equational constraints; otherwise, we attempt to use McCallum's projection with Brown's improvement. When the system does not turn out to be well oriented, we compute Hong's projection.
The Lifting Phase of the CAD Algorithm
In the lifting phase, we find a cell decomposition of the semialgebraic set. Generally speaking, although the actual details depend on the projection operator used, we start with cells in 
consisting of all distinct roots of 
and the open intervals between the roots. We find a sample point in each of the cells and remove the cells whose sample points do not satisfy the system describing the semialgebraic set (the system may contain conditions involving only 
). Next we lift the cells to cells in 
, one dimension at a time. Suppose we have lifted the cells to 
. To lift a cell 
to 
, we find the real roots of 
with 
replaced with the coordinates of the sample point 
in 
. Since the polynomials of 
are delineable on 
, each root 
is a value of a continuous algebraic function at 
, and the function can be represented as a 
th root of a polynomial 
such that 
is the 
th root of 
. Now the lifting of the cell 
to 
will consist of graphs of these algebraic functions and of the slices of 
×
between the subsequent graphs. The sample points in each of the new cells will be obtained by adding the 
st coordinate to 
, equal to one of the roots, or to a number between two subsequent roots. As in the first step, we remove those lifted cells whose sample points do not satisfy the system describing the semialgebraic set.
If 
, 
is a quantifier variable and we may not need to construct all the lifted cells. All we need is to find the (necessarily constant) truth value of 
on 
. If 
, we know that the value is True as soon as the truth value of 
on one of the lifted cells is True. If 
, we know that the value is False as soon as the truth value of 
on one of the lifted cells is False.
The coefficients of sample points computed this way are in general algebraic numbers. To save costly algebraic number computations, the Wolfram Language uses arbitrary-precision floating-point number (Wolfram Language "bignum") approximations of the coefficients, whenever the results can be validated. Note that using approximate arithmetic may be enough to prove that two roots of a polynomial or a pair of polynomials are distinct, and to find a nonzero sign of a polynomial at a sample point. What we cannot prove with approximate arithmetic is that two roots of a polynomial or a pair of polynomials are equal, or that a polynomial is zero at a sample point. However, we can often use information about the origins of the cell to resolve these problems. For instance, if we know that the resultant of two polynomials vanishes on the cell, and these two polynomials have exactly one pair of complex roots that can be equal within the precision bounds, we can conclude that these roots are equal. Similarly, if the last coordinate of a sample point was a root of a factor of the given polynomial, we know that this polynomial is zero at the sample point. If we cannot resolve all the uncertainties using the collected information about the cell, we compute the exact algebraic number values of the coordinates. For more details, see [14, 24].
Decision Problems, FindInstance, and Assumptions
A decision problem is a system with all variables existentially quantified, that is, a system of the form
where 
are all variables in 
. Solving a decision problem means deciding whether it is equivalent to True or to False, that is, deciding whether the quantifier-free system of polynomial equations and inequalities 
has solutions.
All algorithms used by the Wolfram Language to solve real polynomial decision problems are capable of producing a point satisfying 
if the system has solutions. Therefore the algorithms discussed in this section are used not only in Reduce and Resolve for decision problems, but also in FindInstance, whenever a single instance is requested and the system is quantifier free or contains only existential quantifiers. The algorithms discussed here are also used for inference testing by Wolfram Language functions using assumptions such as Simplify, Refine, Integrate, and so forth.
contains the disk of radius 4/5 centered at the origin:
does not contain the unit disk and provides a counterexample: a point in the unit disk that does not belong to 
:The primary method that allows the Wolfram Language to solve arbitrary real polynomial decision problems is the Cylindrical Algebraic Decomposition (CAD) algorithm. There are, however, several other special case algorithms that provide much better performance in cases in which they are applicable.
When all polynomials are linear with rational number or floating-point number coefficients, the Wolfram Language uses a method based on the simplex linear programming method. For other linear systems, the Wolfram Language uses a variant of the Loos–Weispfenning linear quantifier elimination algorithm [15]. When the system contains no equations and only strict inequalities, a faster "generic" version of CAD is used [12, 13]. For systems containing equational constraints that generate a zero-dimensional ideal, the Wolfram Language uses Gröbner bases to find a solution. For nonlinear systems with floating-point number coefficients, an inexact coefficient version of CAD [16] is used.
There are also some special case methods that can be used as preprocessors to other decision methods. When the system contains an equational constraint linear with a constant coefficient in one of the variables, the constraint is used to eliminate the linear variable. If there is a variable that appears in the system only linearly with constant coefficients, the variable is eliminated using the Loos–Weispfenning linear quantifier elimination algorithm [15]. If there is a variable that appears in the system only quadratically, the quadratic case of Weispfenning's quantifier elimination by virtual substitution algorithm [22, 23] could be used to eliminate the variable. For some examples this gives a substantial speedup; however, quite often it results in a significant slowdown. By default, the algorithm is not used as a preprocessor. Setting the system option QVSPreprocessor in the InequalitySolvingOptions group to True makes the Wolfram Language use it.
There are two other special cases of real decision algorithms available in the Wolfram Language. An algorithm by Aubry, Rouillier, and Safey El Din [17] applies to systems containing only equations. There are examples for which the algorithm performs much better than CAD; however, for randomly chosen systems of equations, it seems to perform significantly worse; therefore, it is not used by default. Setting the system option ARSDecision in the InequalitySolvingOptions group to True causes the Wolfram Language to use the algorithm. Another algorithm by G. X. Zeng and X. N. Zeng [18] applies to systems that consist of a single strict inequality. Again, the algorithm is faster than CAD for some examples, but slower in general; therefore, it is not used by default. Setting the system option ZengDecision in the InequalitySolvingOptions group to True causes the Wolfram Language to use the algorithm.
Arbitrary Real Polynomial Systems
Solving Real Polynomial Systems
According to Tarski's theorem [2], the solution set of an arbitrary (quantified) real polynomial system is a semialgebraic set. Reduce gives a description of this set in the solved form (4).
Quantifier Elimination
The objective of Resolve with no variables specified is to eliminate quantifiers and produce an equivalent quantifier-free formula. The formula may or may not be in a solved form, depending on the algorithm used.
, 
, and 
appearing in the input. However, since 
appears in the input polynomials only linearly, the quantifier can be quickly eliminated using the Loos–Weispfenning linear quantifier elimination algorithm, which depends very little on the complexity of coefficients:Algorithms
The primary method used by the Wolfram Language for solving real polynomial systems and real quantifier elimination is the CAD algorithm. There are, however, simpler methods applicable in special cases.
If the system contains an equational constraint in a variable from the innermost quantifier, the constraint is used to simplify the system using the identity
Note that if 
or 
is a nonzero constant, this eliminates the variable 
.
If all polynomials in the system are linear in a variable from the innermost quantifier, the variable is eliminated using the Loos–Weispfenning linear quantifier elimination algorithm [15].
If all polynomials in the system are at most quadratic in a variable from the innermost quantifier, the variable is eliminated using the quadratic case of Weispfenning's quantifier elimination by virtual substitution algorithm [22, 23]. With the default setting of the system option QuadraticQE, the algorithm is used for Resolve with no variables specified and with at least two parameters present, and for Reduce and Resolve with at least three variables as long as elimination of one variable at most doubles the LeafCount of the system.
The CAD algorithm is used when the previous three special case methods are no longer applicable, but there are still quantifiers left to eliminate or a solution is required.
For systems containing equational constraints that generate a zero-dimensional ideal, the Wolfram Language uses Gröbner bases to find the solution set.
Options
The Wolfram Language functions for solving real polynomial systems have a number of options that control the way that they operate. This section gives a summary of these options.
option name | default value | |
| Cubics | False | whether the Cardano formulas should be used to express numeric solutions of cubics |
| Quartics | False | whether the Cardano formulas should be used to express numeric solutions of quartics |
| WorkingPrecision | ∞ | the working precision to be used in computations |
Reduce, Resolve, and FindInstance options affecting the behavior for real polynomial systems.
Cubics and Quartics
the third radical solution is real, but for 
the first radical solution is real:WorkingPrecision
The setting of WorkingPrecision affects the lifting phase of the CAD algorithm. With a finite working precision prec, sample points in the first variable lifted are represented as arbitrary-precision floating-point numbers with prec digits of precision. When we compute sample points for subsequent variables, we find roots of polynomials whose coefficients depend on already computed sample point coordinates and therefore may be inexact. Hence coordinates of sample points will have precision prec or lower. Determining the sign of polynomials at sample points is simply done by evaluating Sign of the floating-point number obtained after the substitution. Using a finite WorkingPrecision may allow getting the answer faster; however, the answer may be incorrect or the computation may fail due to loss of precision.
ReduceOptions Group of System Options
Here are the system options from the ReduceOptions group that may affect the behavior of Reduce, Resolve, and FindInstance for real polynomial systems. The options can be set with
SetSystemOptions["ReduceOptions"->{"option name"->value}].
option name | default value | |
| "AlgebraicNumberOutput" | True | whether Reduce should output AlgebraicNumber objects instead of polynomials in one Root object |
| "FactorEquations" | Automatic | whether equations should be factored at the input preprocessing stage |
| "FactorInequalities" | False | whether inequalities should be factored at the input preprocessing stage |
| "ReorderVariables" | Automatic | whether Reduce, Resolve, and Solve are allowed to reorder the specified variables |
| "UseNestedRoots" | Automatic | whether Root objects representing algebraic numbers defined by triangular systems of equations can be used in the output |
ReduceOptions group options affecting the behavior of Reduce, Resolve, and FindInstance for real polynomial systems.
For systems with equational constraints generating a zero-dimensional ideal 
, the Wolfram Language uses a variant of the CAD algorithm that finds projection polynomials using Gröbner basis methods. If the lexicographic order Gröbner basis of 
contains linear polynomials with constant coefficients in every variable but the last one (which is true "generically"), then all coordinates of a solution are polynomials in one algebraic number, namely the last coordinate. The setting of AlgebraicNumberOutput determines whether Reduce represents the solution coordinates as AlgebraicNumber objects in the field generated by the last coordinate.
The option FactorEquations specifies whether the transformation
should be used at the input preprocessing stage. With the default setting FactorEquations->Automatic, the decision is made by an automatic heuristic.
at the input preprocessing stage may speed up the computations in some cases. In general, however, it does not make the problem easier to solve, and, in some cases, it may make the problem significantly harder. By default, these transformations are not used.
first and express 
in terms of the solution for 
:InequalitySolvingOptions Group of System Options
Here are the system options from the InequalitySolvingOptions group that may affect the behavior of Reduce, Resolve, FindInstance, and CylindricalDecomposition for real polynomial systems. The options can be set with
SetSystemOptions["InequalitySolvingOptions"->{"option name"->value}].
option name | default value | |
| "ARSDecision" | False | whether to use the decision algorithm given in [17] |
| "BrownProjection" | True | whether the CAD algorithm should use the improved projection operator given in [8] |
| "CAD" | True | whether to use the CAD algorithm |
| "CADBacksubstitution" | Automatic | whether the CAD algorithm should backsubstitute numeric values of solution coordinates |
| "CADCombineCells" | True | whether the output of the CAD algorithm should be simplified by combining adjacent cells over which the solution formulas are identical |
| "CADConstruction" | Automatic | specifies the CAD construction method |
| "CADDefaultPrecision" | 30.103 | the initial precision to which nonrational roots are computed in the lifting phase of the CAD algorithm; if the computation with approximate roots cannot be validated, the algorithm raises the precision by the value of "CADExtraPrecision"; if this does not resolve the issue, the algorithm reverts to exact algebraic number computation |
| "CADExtraPrecision" | 30.103 | the amount of extra precision to be used in the lifting phase of the CAD algorithm |
| "CADMethod" | Automatic | specifies the CAD computation method used by CylindricalDecomposition |
| "CADSortVariables" | Automatic | whether the CAD algorithm should use variable reordering heuristics for quantifier variables within a single quantifier or in decision problems |
| "CADZeroTest" | {0,∞} | determines the zero testing method used by the CAD algorithm for expressions obtained by evaluating polynomials at points with algebraic number coordinates |
| "EquationalConstraintsCAD" | Automatic | whether the projection phase of the CAD algorithm should use equational constraints; with the default Automatic setting the operator proven correct in [11] is used; if True the unproven projection operator using multiple equational constraints suggested in [4] is used |
| "FGLMBasisConversion" | False | whether the CAD algorithm should use a Gröbner basis conversion algorithm based on [20] to find univariate polynomials in zero-dimensional Gröbner bases; otherwise, GroebnerWalk is used |
| "FGLMElimination" | Automatic | whether the decision and quantifier elimination algorithms for systems with equational constraints forming a zero-dimensional ideal should use an algorithm based on [20] to look for linear equation constraints (with constant leading coefficients) in one of the variables to be used for elimination |
| "GenericCAD" | True | whether to use the variant of the CAD algorithm described in [13] for decision and optimization problems |
| "GroebnerCAD" | True | whether the CAD algorithm for systems with equational constraints forming a zero-dimensional ideal should use Gröbner bases as projection |
| "LinearDecisionMethodCrossovers" | ||
| {0,30,20,Automatic} | determines methods used to find solutions of systems of linear equations and inequalities with rational number coefficients | |
| "LinearEquations" | True | whether to use linear equation constraints (with constant leading coefficients) to eliminate variables in decision problems |
| "LinearQE" | True | whether to use the Loos–Weispfenning linear quantifier elimination algorithm [15] for quantifier elimination problems |
| "LWDecision" | True | whether to use the Loos–Weispfenning linear quantifier elimination algorithm [15] for decision problems with linear inequality systems |
| "LWPreprocessor" | Automatic | whether to use the Loos–Weispfenning linear quantifier elimination algorithm [15] as a preprocessor for the decision problems |
| "ProjectAlgebraic" | Automatic | whether the CAD algorithm should compute projections with respect to variables replacing algebraic number coefficients or use their minimal polynomials instead |
| "ProveMultiplicities" | True | determines the way in which the lifting phase of the CAD algorithm validates multiple roots and zero leading coefficients of projection polynomials |
| "QuadraticQE" | Automatic | whether to use the quadratic case of Weispfenning's quantifier elimination by virtual substitution algorithm in quantifier elimination |
| "QVSPreprocessor" | False | whether to use the quadratic case of Weispfenning's quantifier elimination by virtual substitution algorithm as a preprocessor for the decision problems |
| "ReducePowers" | Automatic | whether to replace  with  in the input to the CAD, where  is the GCD of all exponents of  in the system |
| "RootReduced" | False | whether the coordinates of solutions of systems with equational constraints forming a zero-dimensional ideal should be reduced to single Root objects |
| "Simplex" | True | whether to use the simplex algorithm in the decision algorithm for linear inequality systems |
| "SimplifyInequalities" | Automatic | whether to use the inequality simplification heuristic presented in [25] |
| "ThreadOr" | True | whether to solve each case of disjunction separately in decision problems, optimization, and in quantifier elimination of existential quantifiers when the quantifier-free system does not need to be solved |
| "ZengDecision" | False | whether to use the decision algorithm given in [18] |
InequalitySolvingOptions group options affecting the behavior of Reduce, Resolve, and FindInstance for real polynomial systems.
is the same for all real 
, even though the solution set is not connected:
and 
have a common root at 
, but have no common roots at other points of the interval 
:The setting of CADConstruction determines the method used for direct CAD construction in all functions using the CAD algorithm. The Wolfram Language contains implementations of two different CAD construction algorithms. With CADConstruction"GlobalProjection", a common projection is computed once and is used for construction of all cells [4, 24]. With CADConstruction"LocalProjection", a local projection is computed for each cell [28]. With CADConstruction"Parallel", two subkernels are launched, and both methods are tried in parallel. With the default setting CADConstructionAutomatic, if at least two subkernels are available, then both methods are tried in parallel; otherwise, a heuristic is used to choose a method.
The setting of CADMethod determines the CAD computation method used by CylindricalDecomposition. It does not affect other functions using the CAD algorithm. The default setting CADMethod->Automatic is a combination of the Direct and Recursive settings.
The setting of this option affects the lifting phase of the CAD algorithm when sample points with exact algebraic number coordinates are used. By default the Wolfram Language uses sample points with arbitrary-precision floating-point number coordinates and validates the results using the methods of [14, 24]. Sample points with exact algebraic number coordinates are used only if the results of approximate computation cannot be validated or if CADDefaultPrecision is set to Infinity.
To determine the sign of a polynomial evaluated at a sample point with algebraic number coordinates, we first evaluate the polynomial at numeric approximations of the algebraic numbers. If the result is nonzero (that is, zero is not within the error bounds of the resulting approximate number), we know the sign. Otherwise, we need to test whether a polynomial expression in algebraic numbers is zero. The value of the CADZeroTest option specifies what zero testing method should be used at this moment. The value should be a pair 
. With the default value 
the Wolfram Language computes an accuracy 
such that if the expression is zero up to this accuracy, it must be zero. If 
, the value of the expression is computed up to accuracy 
and its sign is checked. Otherwise, the expression is represented as a single Root object using RootReduce and the sign of the Root object is found. With the default value 
we revert to RootReduce if eacc>$MaxPrecision. If 
, RootReduce is always used. If 
, expressions that are zero up to accuracy 
are considered zero. This is the fastest method, but, unlike the other two, it may give incorrect results because expressions that are nonzero but close to zero may be treated as zero.
The EquationalConstraintsCAD option specifies whether the projection phase of the CAD algorithm should use equational constraints. With the default setting Automatic, the Wolfram Language uses the projection operator proven correct in [11]. With EquationalConstraintsCAD->True, the smaller but unproven projection operator suggested in [4] is used.
For systems with equational constraints generating a zero-dimensional ideal 
, the Wolfram Language uses a variant of the CAD algorithm that finds projection polynomials using Gröbner basis methods. If the lexicographic order Gröbner basis of 
does not contain linear polynomials with constant coefficients in every variable but the last one and UseNestedRoots is set to False, then for every variable 
we find a univariate polynomial in 
that belongs to 
. The Wolfram Language can do this in two ways. By default, it uses a method based on GroebnerWalk computations. Setting FGLMBasisConversion to True causes the Wolfram Language to use a method based on [20].
The FGLMElimination option specifies whether the Wolfram Language should use a special case heuristic applicable to systems with equational constraints generating a zero-dimensional ideal 
. The heuristic uses a method based on [20] to find in 
polynomials that are linear (with a constant coefficient) in one of the quantified variables and uses such polynomials for elimination. The method can be used both in the decision algorithm and in quantifier elimination. With the default Automatic setting, it is used only in Resolve with no "solve" variables specified and for systems with at least two free variables.
The Wolfram Language uses a simplified version of the CAD algorithm described in [13] to solve decision problems or find solutions of real polynomial systems that do not contain equations. The method finds a solution or proves that there are no solutions if all inequalities in the system are strict (
or 
). The method is also used for systems containing weak (
or 
) inequalities. In this case, if it finds a solution of the strict inequality version of the system, it is also a solution of the original system. However, if it proves that the strict inequality version of the system has no solutions, the full version of the CAD algorithm is needed to decide whether the original system has solutions. The system option GenericCAD specifies whether the Wolfram Language should use the method.
For systems with equational constraints generating a zero-dimensional ideal 
, the Wolfram Language uses a variant of the CAD algorithm that finds projection polynomials using Gröbner basis methods. Setting GroebnerCAD to False, causes the Wolfram Language to use the standard CAD projection instead.
These three options specify methods used to solve decision problems or find solution instances for systems of linear equations and inequalities. The available methods are the Loos–Weispfenning algorithm [15], the simplex algorithm, and the revised simplex algorithm. All three methods can handle systems with rational or floating-point number coefficients. For systems with exact numeric nonrational coefficients, only the Loos–Weispfenning algorithm is implemented. LWDecision specifies whether the Loos–Weispfenning algorithm is available. Simplex specifies whether the simplex and revised simplex algorithms can be used. LinearDecisionMethodCrossovers determines which method is used if all are available and applicable. The value of the option should be a list 
. For linear systems with up to 
variables, the Wolfram Language uses the Loos–Weispfenning method [15]; for systems with 
to 
variables, the simplex algorithm; and for more than 
variables, the revised simplex algorithm. If the simplex algorithm is used, the slack variables are used if the number of inequalities is no more than 
times the number of variables and either 
is True or 
is Automatic and the system is exact. The default values are 
, 
, 
, and s==Automatic.
The LinearEquations option specifies whether linear equation constraints with constant leading coefficients should be used to eliminate variables. This generally improves the performance of the algorithm. The option is provided to allow experimentation with the "pure" CAD-based decision algorithm.
before using CAD to find a solution of the resulting system with two variables:The LinearQE option specifies methods used to handle systems containing at least one innermost quantifier variable that appears at most linearly in all equations and inequalities in the system. The option setting does not affect solving of decision problems. With the default setting True, the Wolfram Language uses the Loos–Weispfenning algorithm [15] to eliminate all quantifier variables that appear only linearly in the system, and then if there are any quantifiers left or the result needs to be solved for the free variables, the CAD algorithm is used. With LinearQE->Automatic, the Loos–Weispfenning algorithm is used only for variables that appear in the system only linearly with constant coefficients. With LinearQE->False, the Loos–Weispfenning algorithm is not used.
and 
, and CAD is used to solve the remaining quantifier-free system with two variables:
, and CAD is used to solve the remaining system with three variables. For this example, the default method is much faster:
and 
, and CAD is used to solve the remaining system with one quantified and one free variable:
, and then CAD is used to solve the remaining system with two quantified variables and one free variable:The LWPreprocessor option setting affects solving decision problems and instance finding. The option specifies whether the Loos–Weispfenning algorithm [8] should be used to eliminate variables that appear at most linearly in all equations and inequalities before applying the CAD algorithm to the resulting system. With the default setting Automatic, the Wolfram Language uses the Loos–Weispfenning algorithm to eliminate variables that appear only linearly with constant coefficients. With LWPreprocessor->True, the Loos–Weispfenning algorithm is used for all variables that appear only linearly. With LWPreprocessor->False, the Loos–Weispfenning algorithm is not used as a preprocessor to the CAD-based decision algorithm.
, and CAD is used to find a solution of the remaining system with three variables:
and 
, and CAD is used to find a solution of the remaining system with two variables. For this example, this method is slower than the default one:
, and CAD is used to find a solution of the remaining system with three variables:
and 
, and CAD is used to find a solution of the remaining system with two variables. For the revised example, this method is faster than the default one:The setting of the ProjectAlgebraic option affects handling of algebraic number coefficients in the CAD algorithm.
Algebraic numbers found in coefficients of the input system are replaced with new variables. The new variables are always put first in the variable ordering so that in the projection phase of the CAD algorithm they are eliminated last. When the current projection polynomials contain 
variables with at least 
first variables replacing algebraic number coefficients, we have a choice of whether or not to continue the projection phase. If we do not continue the projection phase, we can start the lifting phase extending the zero-dimensional cell in the first 
variables on which each of the variables is equal to the corresponding algebraic number coefficient. If we choose to compute the last 
projections, we may find in the lifting phase that the algebraic number coefficient corresponding to a variable being lifted lies between the roots of the projection polynomials. Hence for this variable we will be extending a one-dimensional cell with a rational number sample point. Thus there is a tradeoff between avoiding computation of the last 
projections and avoiding algebraic number coordinates in sample points.
With ProjectAlgebraic->True, the projection phase is continued for variables replacing algebraic number coefficients until there is one variable left. With ProjectAlgebraic->False, the projection phase is stopped as soon as there is one variable left that does not replace an algebraic number coefficient. With the default setting ProjectAlgebraic->Automatic, the projection phase is stopped if there is at most one variable left that does not replace an algebraic number coefficient and there are at least three projection polynomials, or there is a projection polynomial of degree more than two in the projection variable.
The setting of ProveMultiplicities determines the way in which the lifting phase of the CAD algorithm validates multiple roots and zero leading coefficients of projection polynomials obtained using arbitrary-precision floating-point number (Wolfram Language "bignum") computations (for more details, see [14, 24]). With the default setting ProveMultiplicities->True, the Wolfram Language uses information about the origins of the cell, if this is not sufficient computes exact values of cell coordinates and uses principal subresultant coefficients and exact zero testing, and only if this fails reverts to exact computations. With ProveMultiplicities->Automatic, the Wolfram Language uses information about the origins of the cell and, if this is not sufficient, reverts to exact computation. With ProveMultiplicities->False, the Wolfram Language reverts to exact computation each time bignum computations fail to separate all roots or prove that the leading coefficients of projection polynomials are nonzero.
The QuadraticQE option specifies whether the quadratic case of Weispfenning's quantifier elimination by virtual substitution algorithm [22, 23] should be used to eliminate quantified variables that appear at most quadratically in all equations and inequalities in the system. The complexity of Weispfenning's algorithm depends very little on the number of free variables, unlike the complexity of the CAD algorithm that is doubly exponential in the number of all variables. Hence, it is definitely advantageous to use it when all quantifiers can be eliminated using the algorithm, there are many free variables present, and the quantifier-free version of the system does not need to be given in a solved form. On the other hand, eliminating a variable using Weispfenning's algorithm often significantly increases the size of the formula. So if the Wolfram Language needs to apply CAD to the result or if the system contains few free variables, using CAD on the original system may be faster. With the default setting Automatic, the Wolfram Language uses the algorithm for Resolve with no variables specified and with at least two parameters present, and for Reduce and Resolve with at least three variables as long as elimination of one variable at most doubles the LeafCount of the system. This criterion seems to work reasonably well; however, for some examples it does not give the optimal choice of the algorithm. Changing the option value may allow problems to be solved which otherwise take a very long time. With QuadraticQE->True, Weispfenning's algorithm is used whenever there is a quadratic variable to eliminate, with QuardaticQE->False, Weispfenning's algorithm is not used.
. The result is not solved for the parameters 
, 
, and 
:
and then CAD to solve the quantifier-free formula for the parameters 
, 
, and 
. In this example this is faster than the default method of using CAD from the beginning:The QVSPreprocessor option setting affects solving decision problems and instance finding. The option specifies whether the quadratic case of Weispfenning's quantifier elimination by virtual substitution algorithm [22, 23] should be used to eliminate variables that appear at most quadratically in all equations and inequalities before applying the CAD algorithm to the resulting system. The default setting is False and the algorithm is not used. There are examples where using Weispfenning's algorithm as a preprocessor significantly helps the performance, and there are examples where using the preprocessor significantly hurts the performance. It seems that the preprocessor tends to help in examples with many variables and where instances exist. With QVSPreprocessor->True, Weispfenning's algorithm is used each time there is a quadratic variable. With QVSPreprocessor->Automatic, the Wolfram Language uses the algorithm for systems with at least four variables.
For any variable 
in the input to the CAD algorithm, if all powers of 
appearing in the system are integer multiples of an integer 
, the Wolfram Language replaces 
in the input system with a new variable, runs the CAD on the new system, and then resolves the answer so that it is expressed in terms of the original variables. Setting ReducePowers->False turns off this shortcut. With ReducePowers->False, the algebraic functions appearing as cell bounds in the output of the CAD algorithm are always rational functions, quadratic radical expressions, or Root objects. With the default setting ReducePowers->True, they may in addition be 
for any of the previous expressions 
, or Root[a#n-e&,1] for some integer 
, and a rational function or a quadratic radical expression 
.
and 
, and then the result is represented in terms of 
and 
. The result contains Root objects with quadratic radical expressions inside:For systems with equational constraints generating a zero-dimensional ideal 
, the Wolfram Language uses a variant of the CAD algorithm that finds projection polynomials using Gröbner basis methods. If the lexicographic order Gröbner basis of 
contains linear polynomials with constant coefficients in every variable but the last one (which is true "generically"), then all coordinates of solutions are easily represented as polynomials in the last coordinate. Otherwise the coordinates are given as Root objects representing algebraic numbers defined by triangular systems of equations. Setting RootReduced to True causes the Wolfram Language to represent each coordinate as a single numeric Root object defined by a minimal polynomial and a root number. Computing this reduced representation often takes much longer than solving the system.
as a single Root object. However, the computation takes more time:
as a Root object defined by a minimal polynomial and a root number. However, the computation takes more time:With the default setting SimplifyInequalities->Automatic, the Wolfram Language uses the inequality simplification heuristic presented in [25] to simplify inputs to the CAD algorithm, deduce inequalities on CAD projection factors, and use the inequalities to recognize nonzero coefficients and subresultants in the projection phase and to eliminate cells in the lifting phase. The heuristic is also used to simplify intermediate results in the virtual substitution algorithms [15, 23]. Setting SimplifyInequalities to True makes the inequality simplification heuristic perform an additional transformation 
. With SimplifyInequalities->False, the inequality simplification heuristic is not used.
The ThreadOr option specifies how the identity
should be used in the decision algorithm (Reduce and Resolve for systems containing no free variables or parameters), FindInstance, and quantifier elimination (Resolve with no variables specified). With the default setting ThreadOr->True, the identity (8) is used before attempting any solution algorithms. With ThreadOr->False, the identity (8) may be used by algorithms that require using it (for instance, the simplex algorithm), but will not be used by algorithms that do not require using it (for instance, the CAD algorithm).