Algebraic Calculations
Algebraic Calculations
One of the important features of the Wolfram System is that it can do symbolic, as well as numerical calculations. This means that it can handle algebraic formulas as well as numbers.
The Wolfram System automatically carries out basic algebraic simplifications. Here it combines 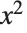 and
and 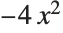 to get
to get 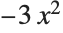 :
:
You can type in any algebraic expression, using the operators listed in "Arithmetic". You can use spaces to denote multiplication. Be careful not to forget the space in xy. If you type in xy with no space, the Wolfram Language will interpret this as a single symbol, with the name xy, not as a product of the two symbols x and y.
The function Expand multiplies out products and powers:
When you type in more complicated expressions, it is important that you put parentheses in the right places. Thus, for example, you have to give the expression 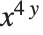 in the form x^(4y). If you leave out the parentheses, you get
in the form x^(4y). If you leave out the parentheses, you get 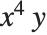 instead. It never hurts to put in too many parentheses, but to find out exactly when you need to use parentheses, look at "Operator Input Forms".
instead. It never hurts to put in too many parentheses, but to find out exactly when you need to use parentheses, look at "Operator Input Forms".
When you type in an expression, the Wolfram System automatically applies its large repertoire of rules for transforming expressions. These rules include the standard rules of algebra, such as 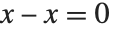 , together with much more sophisticated rules involving higher mathematical functions.
, together with much more sophisticated rules involving higher mathematical functions.
The Wolfram System knows no rules for this expression, so it leaves the expression in the original form you gave:
The notion of transformation rules is a very general one. In fact, you can think of the whole of the Wolfram System as simply a system for applying a collection of transformation rules to many different kinds of expressions.
The general principle that the Wolfram System follows is simple to state. It takes any expression you input, and gets results by applying a succession of transformation rules, stopping when it knows no more transformation rules that can be applied.
There are often many different ways to write the same algebraic expression. As one example, the expression 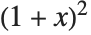 can be written as
can be written as 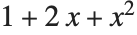 . The Wolfram System provides a large collection of functions for converting between different forms of algebraic expressions.
. The Wolfram System provides a large collection of functions for converting between different forms of algebraic expressions.
| Expand[expr] |
multiply out products and powers, writing the result as a sum of terms
|
| Factor[expr] | write expr as a product of minimal factors |
Expand gives the "expanded form", with products and powers multiplied out:
Factor recovers the original form:
It is easy to generate complicated expressions with Expand:
Factor often gives you simpler expressions:
There are some cases, though, where Factor can give you more complicated expressions:
In this case, Expand gives the "simpler" form:
There are many situations where you want to write a particular algebraic expression in the simplest possible form. Although it is difficult to know exactly what one means in all cases by the "simplest form", a worthwhile practical procedure is to look at many different forms of an expression, and pick out the one that involves the smallest number of parts.
| Simplify[expr] | try to find the simplest form of expr by applying various standard algebraic transformations |
| FullSimplify[expr] | try to find the simplest form by applying a wide range of transformations |
You can often use Simplify to "clean up" complicated expressions that you get as the results of computations.
Differentiating the result from Integrate should give back your original expression. In this case, as is common, you get a more complicated version of the expression:
Simplify succeeds in getting back the original, simpler, form of the expression:
Simplify is set up to try various standard algebraic transformations on the expressions you give. Sometimes, however, it can take more sophisticated transformations to make progress in finding the simplest form of an expression.
FullSimplify tries a much wider range of transformations, involving not only algebraic functions, but also many other kinds of functions.
Simplify does nothing to this expression:
FullSimplify, however, transforms it to a simpler form:
For fairly small expressions, FullSimplify will often succeed in making some remarkable simplifications. But for larger expressions, it can become unmanageably slow.
The reason for this is that to do its job, FullSimplify effectively has to try combining every part of an expression with every other, and for large expressions the number of cases that it has to consider can be astronomically large.
Simplify also has a difficult task to do, but it is set up to avoid some of the most time‐consuming transformations that are tried by FullSimplify. For simple algebraic calculations, therefore, you may often find it convenient to apply Simplify quite routinely to your results.
In more complicated calculations, however, even Simplify, let alone FullSimplify, may end up needing to try a very large number of different forms, and therefore taking a long time. In such cases, you typically need to do more controlled simplification, and use your knowledge of the form you want to get to guide the process.
Some transformations used by Simplify and FullSimplify, for instance reduction with respect to equational assumptions, need to pick an order of variables. Therefore, results of simplification may depend on the names of symbols.
Reduction with respect to the equational assumption using the variable order 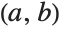 leads to a simplification:
leads to a simplification:
Complicated algebraic expressions can usually be written in many different ways. The Wolfram Language provides a variety of functions for converting expressions from one form to another.
In many applications, the most common of these functions are Expand, Factor, and Simplify. However, particularly when you have rational expressions that contain quotients, you may need to use other functions.
| Expand[expr] | multiply out products and powers |
| ExpandAll[expr] | apply Expand everywhere |
| Factor[expr] | reduce to a product of factors |
| Together[expr] | put all terms over a common denominator |
| Apart[expr] | separate into terms with simple denominators |
| Cancel[expr] | cancel common factors between numerators and denominators |
| Simplify[expr] | try a sequence of algebraic transformations and give the smallest form of expr found |
Expand expands out the numerator, but leaves the denominator in factored form:
ExpandAll expands out everything, including the denominator:
Together collects all the terms together over a common denominator:
Apart breaks the expression apart into terms with simple denominators:
Factor factors everything, in this case reproducing the original form:
According to Simplify, this is the simplest way to write the original expression:
Getting expressions into the form you want is something of an art. In most cases, it is best simply to experiment, trying different transformations until you get what you want. Often you will be able to use palettes in the front end to do this.
When you have an expression with a single variable, you can choose to write it as a sum of terms, a product, and so on. If you have an expression with several variables, there is an even wider selection of possible forms. You can, for example, choose to group terms in the expression so that one or another of the variables is "dominant".
| Collect[expr,x] | group together powers of x |
| FactorTerms[expr,x] | pull out factors that do not depend on x |
As you have seen, even when you restrict yourself to polynomials and rational expressions, there are many different ways to write any particular expression. If you consider more complicated expressions, involving, for example, higher mathematical functions, the variety of possible forms becomes still greater. As a result, it is totally infeasible to have a specific function built into the Wolfram Language to produce each possible form. Rather, the Wolfram Language allows you to construct arbitrary sets of transformation rules for converting between different forms. Many Wolfram Language packages include such rules; the details of how to construct them for yourself are given in "Transformation Rules and Definitions".
There are nevertheless a few additional built‐in Wolfram Language functions for transforming expressions.
| TrigExpand[expr] | expand out trigonometric expressions into a sum of terms |
| TrigFactor[expr] | factor trigonometric expressions into products of terms |
| TrigReduce[expr] | reduce trigonometric expressions using multiple angles |
| TrigToExp[expr] | convert trigonometric functions to exponentials |
| ExpToTrig[expr] | convert exponentials to trigonometric functions |
| FunctionExpand[expr] | expand out special and other functions |
| ComplexExpand[expr] | perform expansions assuming that all variables are real |
| PowerExpand[expr] | transform (xy)p into xpyp, etc. |
The transformations on expressions done by functions like Expand and Factor are always correct, whatever values the symbolic variables in the expressions may have. Sometimes, however, it is useful to perform transformations that are only correct for some possible values of symbolic variables. One such transformation is performed by PowerExpand.
PowerExpand does the expansion:
| Simplify[expr,assum] | simplify expr with assumptions |
The Wolfram Language does not automatically simplify this, since it is only true for some values of x:
| Element[x,dom] | state that x is an element of the domain dom |
| Element[{x1,x2,…},dom] | state that all the xi are elements of the domain dom |
| Reals | real numbers |
| Integers | integers |
| Primes | prime numbers |
| Coefficient[expr,form] | coefficient of form in expr |
| Exponent[expr,form] | maximum power of form in expr |
| Part[expr,n] or expr[[n]] | n th term of expr |
You may notice that the function Part[expr,n] used to pick out the n th term in a sum is the same as the function described in "Manipulating Elements of Lists" for picking out elements in lists. This is no coincidence. In fact, as discussed in "Manipulating Expressions like Lists", every Wolfram Language expression can be manipulated structurally much like a list. However, as discussed in "Manipulating Expressions like Lists", you must be careful, because the Wolfram Language often shows algebraic expressions in a form that is different from the way it treats them internally.
Coefficient works even with polynomials that are not explicitly expanded out:
| Numerator[expr] | numerator of expr |
| Denominator[expr] | denominator of expr |
Denominator picks out the denominator:
When you do symbolic calculations, it is quite easy to end up with extremely complicated expressions. Often, you will not even want to see the complete result of a computation.
If you end your input with a semicolon, the Wolfram Language will do the computation you asked for, but will not display the result. You can nevertheless use % or Out[n] to refer to the result.
By default, the Wolfram System front end will display any outputs which are excessively large in a shortened form inside an interface which allows you to refine the display of the output.
The Show Less and Show More buttons allow you to decrease or increase the level of detail to which the Wolfram System shows the expression. The Show Full Output button removes the interface entirely and displays the full result, but the result may take considerable time to display. The default threshold size at which this feature starts working may be set using the Set Size Limit option, which opens the Preferences dialog to the panel with the appropriate setting.
The large output suppression feature is implemented using the Wolfram Language function Short. You can use Short directly for finer control over the display of expressions. You can also use it for outputs that are not large enough to be suppressed by the default suppression scheme.
Ending your input with ; stops the Wolfram Language from displaying the complicated result of the computation:
You can still refer to the result as %. //Short displays a one‐line outline of the result. The <<n>> stands for n terms that have been left out: