WSMFindEquilibrium
WSMFindEquilibrium["mmodel"]
searches for an equilibrium to the model "mmodel".
WSMFindEquilibrium["mmodel",{{{x1,x10},…},{{u1,u10},…},{{y1,y10},…}}]
searches for an equilibrium, starting from the point xi=xi0, ui=ui0, and yi=yi0.
WSMFindEquilibrium["mmodel",{x1v1,…},…]
searches for an equilibrium, with variable xi constrained to have the value vi etc.
Details and Options
- WSMFindEquilibrium returns a list {{{x1,
 },…},{{u1,
},…},{{u1, },…},{{y1,
},…},{{y1, },…}}, where
},…}}, where  ,
, 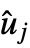 , and
, and  are the computed equilibrium values for states, inputs, and outputs.
are the computed equilibrium values for states, inputs, and outputs. - With no explicit starting point given, WSMModelData["mmodel","GroupedInitialValues"] is used.
- An equilibrium for a differential algebraic system
 is a value
is a value  and
and  such that
such that  .
. - WSMFindEquilibrium will attempt to find a local equilibrium point. In general, many equilibrium points may exist for a system.
- The shortest unique model name mmodel can be used where WSMNames["*.mmodel"] gives a unique match.
- The following options can be given:
-
WSMProgressMonitor Automatic control display of progress
Examples
open allclose allBasic Examples (4)
Scope (3)
Applications (5)
Find an equilibrium point for a single water tank with inflow and outflow:
Linearize a model around an equilibrium point:
Linearize around an equilibrium point and analyze the stability:
Design a PI controller for keeping the level in a tank with inflow and outflow constant:
Find the equilibrium where the level "h" is constrained to be 2:
Linearize and close the loop around a PI controller:
Show the closed-loop step response for a family of PI controllers:
Simple pendulum swinging through any angle:
Equilibrium with the pendulum hanging straight down:
Pendulum standing straight up above its axis:
Level curves of the first integral give the potential energy of the system:
The pendulum has one stable and two unstable equilibrium points:
