|
2.8.5 Options for ApproximateMatrixEquation
ApproximateMatrixEquation can be called with a number of options, most of which are for very advanced usage only and need not be changed unless there appear to be problems with the default settings. Since all options from Options[ApproximateMatrixEquation] are documented in Section 3.11.3, we will restrict ourselves to the discussion of the option SortingMethod. Note that the option CompressEquations has already been introduced in Section 2.8.4.
SortingMethod
ApproximateMatrixEquation removes negligible contributions from a matrix equation term by term following a ranking scheme which causes the term with the smallest influence on the solution to be removed first. The term ranking is obtained by sorting the list of the individual numerical influences of all terms by least influence. If only one design point is present, the sorting order is obvious, but it is not obvious for two or more design points. For example, if removing matrix entry 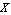 causes a magnitude error of causes a magnitude error of 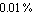 in design point in design point 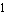 and an error of and an error of 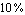 in design point in design point 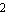 while the error values for matrix entry while the error values for matrix entry 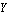 are are 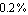 and and 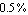 respectively, which entry should be removed first? Removing respectively, which entry should be removed first? Removing 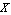 first would introduce a very small error in design point first would introduce a very small error in design point 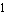 but an excessively large one in design point but an excessively large one in design point 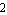 . On the other hand, . On the other hand, 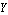 has a much larger influence in design point has a much larger influence in design point 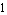 than than 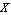 but the total error in both design points would be smaller if but the total error in both design points would be smaller if 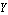 is removed first. is removed first.
SortingMethod is an option which selects the sorting strategy that is applied to the influence list to obtain the term rankings. By default, terms are ranked by least influence on the solution in the primary design point, that is design point 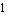 . In the above example, this strategy would give . In the above example, this strategy would give 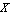 precedence over precedence over 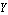 . The corresponding option setting in Options[ApproximateMatrixEquation] is . The corresponding option setting in Options[ApproximateMatrixEquation] is
SortingMethod -> PrimaryDesignPoint
The other available strategy ranks terms by least arithmetic mean influence in all design points, which would give 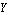 precedence over precedence over 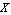 : :
SortingMethod -> LeastMeanInfluence
Usually, LeastMeanInfluence is the better choice if the calculations involve more than one design point. To examine the effect of selecting a different term ranking method we repeat the previous approximation run with SortingMethod -> LeastMeanInfluence.
In[37]:= approxceamp4 = ApproximateMatrixEquation[ceampsta,
V$RL, dpceamp3, CompressEquations -> True,
SortingMethod -> LeastMeanInfluence]
Out[39]= 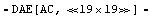
Solving these approximated equations now yields a much simpler expression.
In[38]:= voutsimp4 = V$RL /. First[Solve[approxceamp4, V$RL]]
Out[40]= 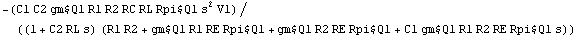
Here, we determined the approximation sequence by using the average of the design-point errors as sorting criterion. In our first approximation run with two design points the term influences on the second design point at 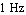 were not taken into consideration when the ranking was computed. The error bound at design point were not taken into consideration when the ranking was computed. The error bound at design point 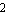 was reached quickly because some terms were removed first which had low influence in design point was reached quickly because some terms were removed first which had low influence in design point 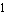 but large influence in design point but large influence in design point 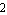 . .
|