|
2.8.4 Combining SBG and SAG
While equation-based approximation can reduce the complexity of a symbolic expression greatly the result may still contain some insignificant terms. So it is generally a good idea to apply solution-based simplification to such a transfer function as well in order to remove the remaining irrelevant contributions. The following example demonstrates the combination of SBG and SAG.
First, we use matrix approximation to compute a reduced-order transfer function of the amplifier from Section 2.8.1 (see Figure 8.1) which is valid for the passband and also for low frequencies. Therefore, we add a second reference point at 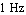 to the list of design points. We allow for an error of up to to the list of design points. We allow for an error of up to 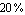 in that point because we do not need high precision there. in that point because we do not need high precision there.
In[29]:= dpceamp3 = {{s -> 2. Pi I 10^4, MaxError -> 0.1},
{s -> 2. Pi I 1, MaxError -> 0.2}};
In the subsequent call to ApproximateMatrixEquation we specify the option CompressEquations -> True. The effect of this option is that all rows and columns of the matrix equation which are not needed to compute the variable of interest will be deleted after approximation. Unlike approximation this is a mathematically exact operation, so no further information will be lost. The benefit gained from compressing a matrix equation is a speed-up in solving the system.
In[30]:= approxceamp3 = ApproximateMatrixEquation[ceampsta,
V$RL, dpceamp3, CompressEquations -> True]
Out[32]= 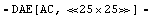
With the CompressEquations option the approximated equations are reduced from a 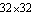 to a to a 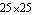 system without changing the symbolic solution for V$RL. The compression factor usually increases with larger matrix sizes and error bounds. Solving the approximated system yields the following expression. system without changing the symbolic solution for V$RL. The compression factor usually increases with larger matrix sizes and error bounds. Solving the approximated system yields the following expression.
In[31]:= voutsimp3 = Together[
V$RL /. First[Solve[approxceamp3, V$RL]]]
Out[33]= 
As compared to the result of our previous equation-based simplification this transfer function is quite lengthy again. Still, approximating the matrix has reduced the degree of the solution. Therefore, we can apply solution-based approximation to compute a simplified transfer function which is more compact than our SAG-only solution and valid over a larger frequency range than our first SBG result.
In[32]:= voutSBGSAG = ApproximateTransferFunction[voutsimp3,
s, dpceamp, 0.1]
Out[34]= 
The common factor which appears in the coefficients of the numerator and the denominator of this transfer function can be cancelled by algebraic simplification:
In[33]:= voutsimp3s = Simplify[voutSBGSAG]
Out[35]= 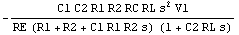
The above result is very useful because it allows for reading off approximate symbolic expressions for the poles. To calculate these explicitly we must solve the denominator of the transfer function for s:
In[34]:= poles = Solve[Denominator[voutsimp3s] == 0, s]
Out[36]= 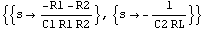
From our SAG-only approximation (voutsimp) alone we cannot determine the poles so easily because the denominator is a polynomial of degree 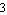 . On the other hand, the SBG-only approximation is too large to yield meaningful expressions for the poles. This shows that combining SBG with SAG techniques can also be a powerful approach for computing other circuit characteristics than only transfer functions. . On the other hand, the SBG-only approximation is too large to yield meaningful expressions for the poles. This shows that combining SBG with SAG techniques can also be a powerful approach for computing other circuit characteristics than only transfer functions.
In[35]:= voutsimp3n[s_] = voutsimp3s /. dpceamp
Out[37]= 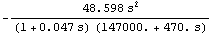
Finally, we plot this simplified transfer function together with the original function to visualize the effects of our low-and-mid-frequency approximation. The Bode plot shows that the approximation is valid from zero frequency to the upper end of the passband at about 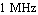 . High-frequency effects are not described because we did not specify a design point in the frequency region beyond the passband. . High-frequency effects are not described because we did not specify a design point in the frequency region beyond the passband.
In[36]:= BodePlot[{voutexactn[2. Pi I f], voutsimp3n[2. Pi I f]},
{f, 1., 1.*10^9}, MagnitudeDisplay -> Linear,
PlotRange -> {{0, 2.5}, Automatic}]
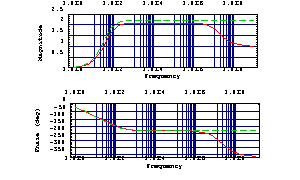
Out[38]= 
|