|
2.8.3 Equation-Based Symbolic Approximation
Coping with the Limit of Solution-Based Approximation Techniques
Solution-based expression approximation techniques have one obvious drawback: they can only be applied to symbolic transfer functions after these have been computed from systems of circuit equations. This precludes the use of SAG techniques in those cases where calculating an unsimplified symbolic transfer function is technically impossible. In practice, the limit is reached very quickly, because even for small analog building blocks with ten or less active devices the term count of the transfer functions can be expected to grow into the millions, if not into billions.
To cope with these cases we must resort to simplification-before-generation techniques which simplify the problem beforehand, i.e. even before a transfer function is computed symbolically. Such simplifications can be done manually on circuit level, for instance by replacing negligible components with zero-admittance or zero-impedance elements. However, as controlling the error introduced by manual simplifications is usually difficult, Analog Insydes provides an automatic and more reliable SBG algorithm which operates on systems of symbolic circuit equations. Hence, it belongs to the class of equation-based approximation techniques.
Given a system of symbolic linear circuit equations in matrix form 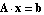 and a design point, the equation-based approximation algorithm implemented in Analog Insydes finds and removes all symbolic matrix entries whose numerical contribution to the design-point value of the transfer function is negligible, thereby keeping track of the accumulated approximation error. As the number of removed matrix entries is usually quite large the solution of the resulting simplified matrix equation will be much less complex than the solution of the unsimplified system. Therefore, we can calculate simplified symbolic transfer functions without ever having to compute the full expressions at all. This will be illustrated by an example right after the following explanations on how to specify design points for the matrix approximation function. and a design point, the equation-based approximation algorithm implemented in Analog Insydes finds and removes all symbolic matrix entries whose numerical contribution to the design-point value of the transfer function is negligible, thereby keeping track of the accumulated approximation error. As the number of removed matrix entries is usually quite large the solution of the resulting simplified matrix equation will be much less complex than the solution of the unsimplified system. Therefore, we can calculate simplified symbolic transfer functions without ever having to compute the full expressions at all. This will be illustrated by an example right after the following explanations on how to specify design points for the matrix approximation function.
Design Points for Matrix Approximation
Since the matrix approximation algorithm can work with multiple design points with individual error bounds, the design points must be specified in a slightly different form as compared to those for solution-based approximation:
designpoint = 
 symbol -> value, symbol -> value,  , MaxError -> , MaxError -> 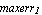  , ,
 symbol -> value, symbol -> value,  , MaxError -> , MaxError -> 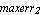 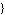 , ,
Note that for symbols which are not specified here the corresponding design-point value is automatically extracted from the design point stored in the DAEObject. Each set of design-point values must be accompanied by a rule with the keyword MaxError on its left-hand side. This rule specifies the maximum relative error by which the magnitude of the solution of the approximated system of equations may deviate from the value of the magnitude of the transfer function in the corresponding design point. The error bound maxerr must be a real number greater than zero. Note that the error definition used here is different from the one used with ApproximateTransferFunction in that it pertains to the total error on the magnitude of the entire transfer function at certain frequencies and not to the error on individual coefficients. It is thus a more reliable error measure than the coefficient error.
Let's define a design point for applying matrix approximation to our double-voltage-divider example (see Figure 8.2 in Section 2.8.1). We can use the same numerical values for the resistors and the voltage source as we did for solution-based approximation. If we allow for up to 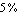 magnitude error of the simplified result with respect to the unsimplified solution we must write the error bound specification as MaxError -> 0.05. Note that although we have only one single design point here we must wrap the list of rules into an additional level of list braces. magnitude error of the simplified result with respect to the unsimplified solution we must write the error bound specification as MaxError -> 0.05. Note that although we have only one single design point here we must wrap the list of rules into an additional level of list braces.
In[20]:= dpdvd = {{MaxError -> 0.05}};
Approximating Symbolic Matrix Equations
Symbolic matrix equations can be approximated by means of the command ApproximateMatrixEquation, which has the following command syntax:
ApproximateMatrixEquation[dae, var, dp, opts]
The first argument dae represents a DAEObject containing small-signal circuit equations in matrix form as returned by CircuitEquations, var specifies the variable for which the equations should be solved after approximation, and dp denotes a list of design points as discussed above. The remaining argument opts is a sequence of options which may also be empty.
We are now ready to try out equation-based approximation on the MNA equations of the voltage divider. For comparison, here are the original unsimplified equations again.
In[21]:= DisplayForm[dvdmna]
Out[22]//DisplayForm= 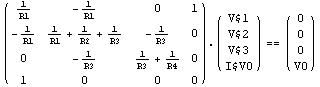
Since we are interested in a simplified solution for the voltage at the output node 3, we specify V$3 as the variable for which the equations are to be approximated.
In[22]:= approxdvd = ApproximateMatrixEquation[dvdmna,
V$3, dpdvd];
DisplayForm[approxdvd]
Out[24]//DisplayForm= 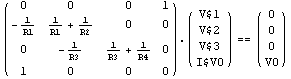
The result is a matrix equation from which all numerical irrelevant symbolic terms have been removed. We can now compute a simplified transfer function directly by solving the approximated equations.
In[23]:= Solve[approxdvd, V$3]
Out[25]= 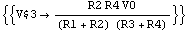
In this case, we obtain identical results from both equation-based and solution-based approximation. However, as opposed to the latter, equation-based approximation does not require an exact symbolic solution to be computed first. In such a small example this advantage makes nearly no difference, but it will turn out to be a key factor in larger applications.
Approximating the Equations of the Amplifier
As an example for a slightly larger application let's continue with our well-known common-emitter amplifier once more. Again, we start by setting up a design point for ApproximateMatrixEquation, reusing the numerical values we defined for simplifying the exact solution with ApproximateTransferFunction. For matrix approximation, however, we still need some more numerical information. While the SAG algorithm approximates the coefficients of a transfer function independently, the SBG method uses the total value of a transfer function in a design point as reference quantity. Therefore, we must specify one or more particular frequency points at which ApproximateMatrixEquation should monitor the change in the value of the transfer function caused by the removal of terms.
Here, we might be interested in computing a simplified expression describing the passband voltage gain of the amplifier. The Bode plot above shows that the passband extends from about 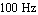 to several to several  , so we choose a design-point value for the operating frequency in the middle of the passband, e.g. at , so we choose a design-point value for the operating frequency in the middle of the passband, e.g. at 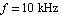 . The corresponding value for the Laplace frequency . The corresponding value for the Laplace frequency 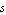 is then given by is then given by 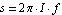 . Finally, we limit the approximation error in this frequency point to . Finally, we limit the approximation error in this frequency point to 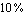 of the original magnitude value. of the original magnitude value.
In[24]:= dpceamp2 = {{s -> 2. Pi I 10^4, MaxError -> 0.1}};
In the next step, we approximate the sparse tableau equations of the amplifier for the given design-point data with respect to the output voltage V$RL.
In[25]:= approxceamp = ApproximateMatrixEquation[ceampsta,
V$RL, dpceamp2]
Out[27]= 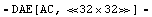
Then we solve the approximated system for V$RL to obtain a simplified voltage transfer function.
In[26]:= voutsimp2 = (V$RL / V1) /. First[Solve[approxceamp, V$RL]]
Out[28]= 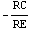
By equation-based approximation we have reduced the symbolic transfer function to the simple quotient of two resistor values. In comparison to the original transfer function, which is composed of more than 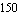 terms, this may seem to be a rather surprising result. From a technical point of view, however, the extreme reduction of complexity is not surprising at all because the amplifier was designed to have a voltage gain of approximately terms, this may seem to be a rather surprising result. From a technical point of view, however, the extreme reduction of complexity is not surprising at all because the amplifier was designed to have a voltage gain of approximately 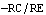 . Therefore, our approximate symbolic analysis just extracted knowledge which was put into this circuit structure at the time of its design. . Therefore, our approximate symbolic analysis just extracted knowledge which was put into this circuit structure at the time of its design.
Again, we evaluate the simplified expression with the design-point values and compare the result with the original transfer function.
In[27]:= voutsimp2n[s_] = voutsimp2 /. dpceamp
Out[29]= 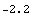
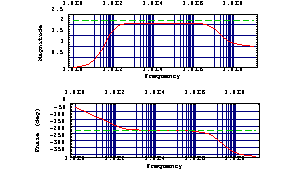
In[28]:= BodePlot[{voutexactn[2. Pi I f], voutsimp2n[2. Pi I f]},
{f, 1., 1.*10^9}, MagnitudeDisplay -> Linear,
PlotRange -> {{0, 2.5}, Automatic}]
Out[30]= 
It becomes immediately apparent from the plots that the result obtained by means of SBG does not constitute a global description of the frequency response of the amplifier. As opposed to the SAG solution, the SBG solution is only valid in the passband region and does not reflect the behavior the amplifier exhibits for very low or very high frequencies. But remember that such a local approximation was precisely what we asked for because we specified only one reference point on the frequency axis at 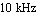 . .
Equation-based approximation thus allows us to compute reduced-order circuit models for limited frequency ranges. Of course, we can also define several frequency points at which ApproximateMatrixEquation monitors the approximation error in order to extend range of validity of a simplified expression. However, best results in terms of expression complexity are usually obtained through local approximations.
|