|
2.8.2 Solution-Based Symbolic Approximation
Groups of Symbolic Approximation Techniques
Symbolic approximation techniques can be divided into three different groups of methods which perform Simplifications Before, During, or After the Generation of symbolic formulas (SBG, SDG, and SAG methods). The approach discussed above is thus an SAG, or solution-based, method because we computed the complete transfer function first and then simplified it. While the principle behind this SAG technique was demonstrated on the transfer function of a non-dynamic system it can be applied to general transfer functions containing powers of the frequency variable 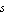 as well. In this case, all symbolic coefficients of the different powers of as well. In this case, all symbolic coefficients of the different powers of 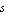 are simplified separately up to a given maximum error. are simplified separately up to a given maximum error.
Approximating Transfer Functions
Analog Insydes provides the function ApproximateTransferFunction for solution-based symbolic approximation. The argument sequence is
ApproximateTransferFunction[tfunc, fvar, dp, maxerr]
where 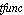 is a rational transfer function in the frequency variable fvar, dp is a design-point specification, and maxerr is the maximum relative error of the simplified coefficients of fvar in the design point. The design point must be specified as a list of rules which associate numerical values with the symbols in tfunc, and maxerr is a real number between is a rational transfer function in the frequency variable fvar, dp is a design-point specification, and maxerr is the maximum relative error of the simplified coefficients of fvar in the design point. The design point must be specified as a list of rules which associate numerical values with the symbols in tfunc, and maxerr is a real number between 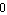 and and 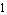 . .
Let's apply solution-based approximation to the transfer function of the common-emitter amplifier calculated in the preceding section. First, we extract the list of design-point values from the DAEObject using GetDesignPoint.
In[15]:= dpceamp = GetDesignPoint[ceampsta]
Out[16]= 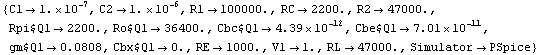
Then we let ApproximateTransferFunction remove all numerical insignificant terms from the coefficients of the frequency variable s, thereby allowing for a maximum design-point error of 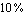 in each coefficient. Note that a in each coefficient. Note that a 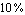 coefficient error does not imply coefficient error does not imply 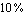 error on the magnitude of the transfer function in the design point. Ideally, the coefficient error should be a common factor and thus cancel from numerator and denominator, yielding zero overall error in the design point. In practice, however, there is no direct correlation between the overall error and the maximum coefficient error. The former is usually lower than the latter but may, in some cases, even be larger. error on the magnitude of the transfer function in the design point. Ideally, the coefficient error should be a common factor and thus cancel from numerator and denominator, yielding zero overall error in the design point. In practice, however, there is no direct correlation between the overall error and the maximum coefficient error. The former is usually lower than the latter but may, in some cases, even be larger.
In[16]:= voutsimp = ApproximateTransferFunction[ceampvout,
s, dpceamp, 0.1] // Together
Out[17]= 
Here, the approximation process reduces the original transfer function to only 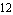 significant terms. We can check the quality of the approximation by evaluating it with the design-point values and comparing it graphically with the original function. significant terms. We can check the quality of the approximation by evaluating it with the design-point values and comparing it graphically with the original function.
In[17]:= voutexactn[s_] = Together[ceampvout /. dpceamp]
Out[18]= 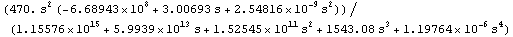
In[18]:= voutsimpn[s_] = voutsimp /. dpceamp
Out[19]= 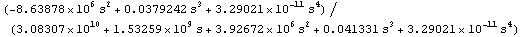
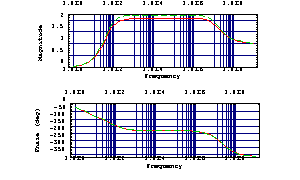
For the following BodePlot we choose a linear scaling of the magnitude values to get a better impression of the true magnitude error. It turns out that the simplified expression (dashed line) approximates the original transfer function (solid line) quite well, although it comprises only about one tenth of the terms of the latter.
In[19]:= BodePlot[{voutexactn[2. Pi I f], voutsimpn[2. Pi I f]},
{f, 1., 1.*10^9}, MagnitudeDisplay -> Linear]
Out[20]= 
|