|
2.8.1 Introduction to Symbolic Approximation
The Complexity Problem
If you have previous experiences with symbolic circuit analysis programs or if you have done some experiments with Analog Insydes before reading this chapter you may have already become aware of a major obstacle which is inherent to symbolic computations. While the carefully selected example circuits analyzed in the preceding chapters all yield transfer functions of no more than a few lines in length minor modifications such as adding an element or two to the circuit or choosing a slightly more complex transistor model may already lead to expressions of incredible size. In fact, expression complexity increases exponentially with the number of symbols in your circuit descriptions, allowing for full symbolic analysis of very small circuits only.
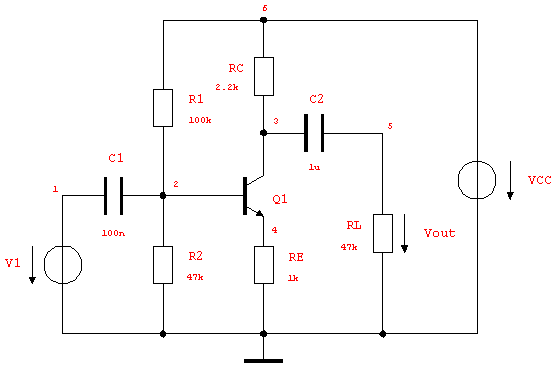
Figure 8.1: Common-emitter amplifier with coupling capacitors and resistive load
Let us demonstrate this effect by computing the symbolic voltage transfer function of the common-emitter amplifier displayed in Figure 8.1. This circuit is essentially the same as the common-emitter amplifier from Section 2.3.1 (see Figure 3.1) except that coupling capacitors and a resistive load have been added.
Following, the netlist description of the circuit is imported via the Analog Insydes command ReadNetlist from already existing simulator files. For more details refer to Section 2.9.2.
In[1]:= <<AnalogInsydes`
In[2]:= ceamp = ReadNetlist[
"AnalogInsydes/DemoFiles/emitter.cir",
"AnalogInsydes/DemoFiles/emitter.out",
KeepPrefix -> False, Simulator -> "PSpice"]
Out[2]= 
From the netlist description, we set up a  system of symbolic sparse tableau equations. We use a complexity-reduced transistor model from the Analog Insydes model library by specifying the option ModelLibrary. system of symbolic sparse tableau equations. We use a complexity-reduced transistor model from the Analog Insydes model library by specifying the option ModelLibrary.
In[3]:= ceampsta = CircuitEquations[ceamp,
ElementValues -> Symbolic, Formulation -> SparseTableau,
ModelLibrary -> "BasicModels`"]
Out[3]= 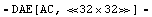
Then we solve the equations for the output voltage V$RL and extract the expression for V$RL from the result.
In[4]:= ceampvout = Together[
V$RL /. First[Solve[ceampsta, V$RL]]]
Out[4]= 
Even for this very small circuit we obtain a transfer function which contains more than 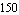 product terms. If you are not impressed yet try calculating the symbolic transfer function of two amplifier stages connected in series, or rather, use ComplexityEstimate to get an estimate of the expression size. product terms. If you are not impressed yet try calculating the symbolic transfer function of two amplifier stages connected in series, or rather, use ComplexityEstimate to get an estimate of the expression size.
Analog Insydes provides the command ComplexityEstimate for computing an estimate of the number of product terms in a transfer function computed from a symbolic matrix equation 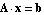 (note that the equations have to be given as a system of AC circuit equations). More precisely, the function computes a lower bound for the number of product terms in the determinant of A. For our common-emitter amplifier this yields the following estimate: (note that the equations have to be given as a system of AC circuit equations). More precisely, the function computes a lower bound for the number of product terms in the determinant of A. For our common-emitter amplifier this yields the following estimate:
In[5]:= ComplexityEstimate[ceampsta]
Out[5]= 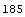
A primary goal of symbolic circuit analysis is to give us qualitative insight into circuit behavior. From a symbolic formula we can read off which circuit elements have an influence on particular circuit characteristics, such as voltage gains or poles and zeros, and we can draw conclusions on how to modify element values in order to make a circuit meet some performance specifications. It is quite obvious, though, that this requires the formulas to be rather small - ideally no more than one line on the screen - because an expression as large as the one above hardly yields any insight. Unfortunately, there is little we can do to reduce the size of symbolic analysis results in a purely algebraic way. Algebraic simplifications such as factoring and cancelling common terms seldom have a sufficiently large impact on expression complexity because transfer functions are usually composed of irreducible polynomials. In addition, factored or partially factored expressions are not necessarily easier to understand than their expanded forms. Exact symbolic analysis is therefore infeasible for most circuits of practical size.
Approximating Symbolic Expressions
There are two ways to cope with the complexity problem. The first one is to keep circuit and device models always as simple as possible. Carefully balancing model accuracy and simplicity holds the key to obtaining meaningful results from symbolic circuit analysis programs, so any knowledge about a particular analysis task should be exploited before running the analyzer. For instance, if our task was to find a symbolic expression describing the voltage gain of the common-emitter amplifier in the passband frequency range for a high-impedance load we should short-circuit the coupling capacitors, neglect the load resistor, and use a transistor model which just meets our accuracy requirements. In other words, to obtain compact results we should model and analyze the circuit exactly like we already did in Chapter 2.3. The major disadvantage of such a-priori simplifications on circuit level is, however, that we cannot always control the final error in our computations which is invariably introduced by neglecting some elements.
The second approach to the generation of interpretable formulas is known as symbolic approximation or symbolic simplification, which refers to a whole family of hybrid symbolic/numeric algorithms for expression simplification. Symbolic approximation techniques require more numerical knowledge about the circuit under examination than manual simplifications but yield compact expressions with predictable error in a fully automatic way. The basic idea behind all these algorithms is to compare the magnitudes of symbolic terms in a transfer function or a system of equations on the basis of numerical reference values and then to discard all those terms which have negligible influence on the result. In most cases, this leads to a dramatic reduction of expression complexity, thus allowing for approximate symbolic analysis of reasonably large circuits.
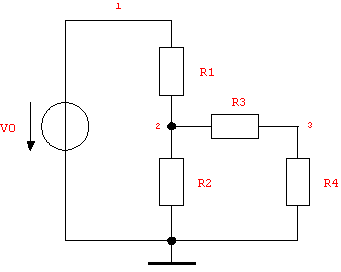
Figure 8.2: Double voltage divider
To understand how symbolic approximation works let's look at a simple example - the transfer function of the double voltage divider shown in Figure 8.2:
In[6]:= doubleVoltageDivider =
Netlist[
{V0, {1, 0}, V0},
{R1, {1, 2}, R1},
{R2, {2, 0}, R2},
{R3, {2, 3}, R3},
{R4, {3, 0}, R4}
]
Out[6]= 
In[7]:= dvdmna = CircuitEquations[doubleVoltageDivider];
DisplayForm[dvdmna]
Out[8]//DisplayForm= 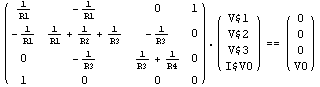
In[8]:= tfdvd = (V$3 / V0) /. First[Solve[dvdmna, V$3]]
Out[9]= 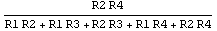
Without any additional knowledge about the circuit this transfer function cannot be simplified much further algebraically. Now, let's assume that in this particular circuit the values of R1 and R2 are approximately equal, as well as those of R3 and R4, but that R1 and R2 have much smaller values than R3 and R4: 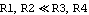 . Under these conditions we can discard the product term . Under these conditions we can discard the product term 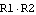 in the denominator of the transfer function because it is the product of two small quantities and thus contributes little to the total value of the expression as compared to the other terms: in the denominator of the transfer function because it is the product of two small quantities and thus contributes little to the total value of the expression as compared to the other terms:
In[9]:= simptfdvd = tfdvd /. R1*R2 -> 0
Out[10]= 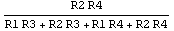
The resulting function can now be factored and simplifies to a more meaningful form.
In[10]:= Factor[simptfdvd]
Out[11]= 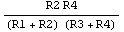
This approximate formula holds for all sets of resistor values for which the condition 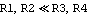 is satisfied, but no longer in the general case. Symbolic approximation thus always implies a trade-off between low expression complexity on the one hand and generality and precision on the other. is satisfied, but no longer in the general case. Symbolic approximation thus always implies a trade-off between low expression complexity on the one hand and generality and precision on the other.
Numerical Reference Values: Design Points
Deciding on which terms to discard from a symbolic expression on the basis of vague information such as "X is much larger than Y" may be feasible for humans but is virtually impossible to do for a computer. This is particularly true when an expression contains a large number of symbols in non-trivial combinations. To enable a computer to reduce a symbolic expression to its dominant content we must provide input which allows for clear yes-or-no decisions on whether a term is important or negligible. This input can be given as a set of accompanying numerical reference values for the symbols, known as a design point, based on which the contributions of compound symbolic terms can be compared numerically. Design-point values need not always be the exact element values for which a circuit works within specifications. However, the reference values should reflect the relative magnitude relations among the symbols in a realistic way.
In the case of the double voltage divider we could express the conditions on the relative magnitudes of the resistors by an (arbitrary) numerical assignment of design-point values such as 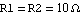 and and 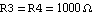 . We rewrite the netlist of the double voltage divider keeping both a symbolic element value and an associated design-point value together in each netlist entry. . We rewrite the netlist of the double voltage divider keeping both a symbolic element value and an associated design-point value together in each netlist entry.
In[11]:= doubleVoltageDivider =
Netlist[
{V0, {1, 0}, Symbolic -> V0, Value -> 1.},
{R1, {1, 2}, Symbolic -> R1, Value -> 10.},
{R2, {2, 0}, Symbolic -> R2, Value -> 10.},
{R3, {2, 3}, Symbolic -> R3, Value -> 1000.},
{R4, {3, 0}, Symbolic -> R4, Value -> 1000.}
]
Out[12]= 
Now, we set up the corresponding equations using the option setting ElementValues -> Symbolic. The design-point values are then automatically stored in the DAEObject and can be extracted via GetDesignPoint.
In[12]:= dvdmna = CircuitEquations[doubleVoltageDivider,
ElementValues -> Symbolic]
Out[13]= 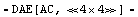
In[13]:= designpoint = GetDesignPoint[dvdmna]
Out[14]= 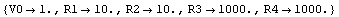
With these reference values we can evaluate the symbolic expression numerically. Below, we apply the function HoldForm to the Plus operation which prevents the denominator from being evaluated to a single number.
In[14]:= tfdvd /. Plus -> HoldForm[Plus] /. designpoint
Out[15]= 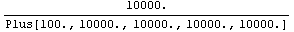
By comparing the individual numerical values we, as well as a computer, can now clearly see that the first argument of the Plus expression, corresponding to the term 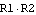 , contributes only , contributes only 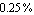 to the total value of the denominator. The term can thus be safely removed from the transfer function if we allow for an error of, say, to the total value of the denominator. The term can thus be safely removed from the transfer function if we allow for an error of, say, 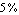 or less in the design point. or less in the design point.
|