2.4.2 ConstraintsThe actual constraint expressions that are generated by SetConstraints can be extracted with Constraints. Constraints can be very useful for debugging a model because it is often possible to read the constraint expressions directly and relate them to the function of the model. Constraints function. This loads the Modeler2D package. Consider the 2D crankshaft-piston model of Section 1.2. This model is built with various settings for the options for SetConstraints to show their affect on the resulting equations. Here is the crankshaft-piston model rebuilt. The first constraint cs[1] is a two degree of freedom constraint that constrains the origin of the crankshaft to lie at the global origin. Here is the expression generated by the Revolute2 constraint.
Out[11]= | 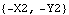 |
Obviously, when these two expressions are driven to zero, the desired result is achieved, the coordinates of the local origin of the crankshaft {X2, Y2} are zero.
The third constraint cs[3] is a two degree of freedom constraint that allows the piston to translate along a vertical axis, but constrains its rotation and its translation in the X direction. Here is the expression generated by the Translate2 constraint.
Out[12]= | 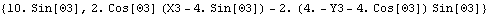 |
The first expression, 10 Sin[ 3], constrains the rotation of the piston; this expression can be equal to zero if 3], constrains the rotation of the piston; this expression can be equal to zero if  3 is any integer multiple of 3 is any integer multiple of  . The reason that the solution . The reason that the solution  3 -> 0 is found is because the default initial guess is 3 -> 0 is found is because the default initial guess is  3 -> 0. If a different initial guess were used, such as 3 -> 0. If a different initial guess were used, such as  3 -> 3, the model would converge to 3 -> 3, the model would converge to  3 -> N[ 3 -> N[ ] instead. ] instead.
The second expression in the list constrains the X coordinate of the piston to be zero. Notice that at any value of  3 that satisfies the first expression, the second expression reduces to 3 that satisfies the first expression, the second expression reduces to 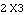 or or 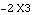 , either of which will drive X3 to zero. , either of which will drive X3 to zero.
|