2.5 Running the ModelThis section covers the use of the SolveMech command, which is used to seek a solution to the mechanism model. The Mech commands covered in the previous sections were all concerned with building a mechanism model. SolveMech is the sole function for running the model. 2.5.1 SolveMechThe SolveMech command is used without arguments to seek a single solution to the mechanism model, with all of the current values of any user-defined variables in the model. When SolveMech seeks a solution, what it is really trying to do is numerically find the location and orientation of each of the bodies in the model at which all of the constraints are satisfied. Mech's runtime command. Time DependenceMost mechanism models have some dependency on time that is specified (by default) by the symbol T. When T appears in a mechanism model, the model's location becomes explicitly a function of time, a technique that must be used in the velocity and acceleration portions of the analysis. It is not necessary to have any dependency on T in a model used only for location analysis, but it is customary to make the primary driving expression a function of T anyway. The symbol for time. SolveMech has several special invocations that are useful for finding a solution or many solutions at a range of values of T. More arguments for SolveMech. The 2D crankshaft-piston model is used to demonstrate the various forms of SolveMech. When this example was first used in Section 1.2, the symbol crankangle was used to specify the rotation of the crankshaft. Now crankangle is replaced with  so that the rotation of the crankshaft is a function of time. Thus, the crankshaft has an angular velocity of one revolution per second. This loads the Modeler2D package. Here is the crankshaft-piston model with a time-dependent driver. Now, instead of changing the value of crankangle to drive the model the value of time is changed directly with SolveMech. This runs the model at 1/10 turn of the crankshaft.
Out[6]= |  |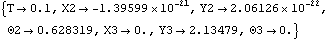
This seeks 3 solutions from 0 to 0.5 turns, inclusive.
Out[7]= |  |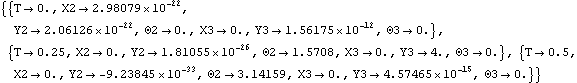
The unusual form of the iteration specifier in SolveMech is very useful if an even spread of data is desired, with a few particular data points specified in between. For example, the following example generates six solution points with the points T = 0., 0.223, and 0.3 included, and the other three points spread so as to fill the gaps as evenly as possible. This seeks 6 solution points, including T = 0.223
Out[8]= |  |
Initial Guesses at RuntimeSetting initial guesses with SolveMech. The primary reason for passing rules into SolveMech, instead of just specifying the value of time, is to accelerate the solution process. The supplied rules may be known to be very good initial guesses, such as rules obtained from a prior run with a slightly different value for a parameter. This calls SolveMech with a list of guesses. The value of time T = 0.2 is pulled from the guesses.
Out[9]= |  |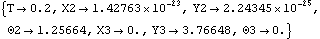
2.5.2 Controlling SolveMechThe nonlinear equation solver used by SolveMech can be controlled by setting the values of several options. Many of these options are the same as those used by FindRoot, although SolveMech does not utilize FindRoot. Options for SolveMech. The operation of SolveMech can be inspected by the use of two hook functions that are called during the execution of SolveMech. Note that all Mech system variables that can be set by the user have names of the form "$Mech*". Controls for SolveMech. Failure to ConvergeThe default setting for ZeroTest will suffice for many models, but may need to be changed for several reasons.
If the numerical size of the dimensions of the model are very large or small, ZeroTest may need to be changed accordingly. For example, if a typical point in the model is Point[2, {3400, -7800}], it might be necessary to specify ZeroTest -> (Abs[#] < 10^-6 &).
If the model is large (eight or more bodies for 2D, four or more for 3D) solving the linear equations at each iteration begins to suffer from numerical error. Thus, it may be necessary to lower the convergence criteria.
The primary indication that the convergence criteria must be changed is that SolveMech returns a valid solution that is apparently correct, but an error message is generated claiming that convergence has failed after n iterations. If the model fails to converge and returns a solution that is obviously not valid, try to find an inconsistency in the constraint set or consult Chapter 13, Debugging Models. 2.5.3 Nonlinear Equation SolverAt the core of Mech's numerical solution block is a Newton-Rhapson simultaneous nonlinear equation solver, similar to the built-in Mathematica function FindRoot. In fact, Mech can be used to solve arbitrary systems of equations that have no relation to mechanism analysis.
Mech's general constraint function Constraint is used to build a constraint object from an arbitrary algebraic equation. The algebraic constraint can be incorporated into a mechanism model along with other geometric constraints, or an entire model can be built from general constraints. The general constraint function. The following uses Mech to find the intersection of a parabola and a circle. This prevents impending spelling errors. This builds the nonmechanical model. This plots the two functions, showing their intersection.
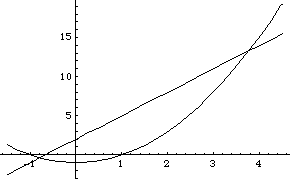
Out[14]= |  |
This seeks a solution to the two equations.
Out[15]= |  |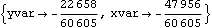
This looks for the other solution.
Out[16]= |  |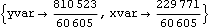
| 
