9.4 Load-Dependent CouplesCoupled systems may be built with mathematical conditions that depend on reaction forces in the mechanism, instead of geometric conditions that depend on body locations and velocities. Such expressions contain the Lagrange multiplier terms (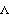 1, 1, 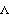 2, ...) that are used to resolve static and dynamic reaction forces in a model. The four-bar mechanism is used to demonstrate this, after adding applied forces and gravity to the model so that the joint reactions are nonzero. 2, ...) that are used to resolve static and dynamic reaction forces in a model. The four-bar mechanism is used to demonstrate this, after adding applied forces and gravity to the model so that the joint reactions are nonzero. 9.4.1 Loads on the Four-Bar ModelThe four-bar mechanism defined in Section 9.1 now has a constant moment applied to the driven bar and gravitational force applied to all bodies. This sets nonzero masses for each body. Here is a clockwise moment applied to the driven bar, and gravity applied to all bodies. 9.4.2 Solving for a ParameterA coupled system is used to find the length of the drive bar that causes the reaction moment at the driving constraint to be equal to 0.5. The driving constraint, number 1, is a RotationLock1 constraint constraining the rotation of the drive bar. Since this constraint only controls the rotation of the drive bar it can support no forces, only a moment. Thus, the reaction force at the constraint is exactly zero. Here is the reaction force and moment that the driving constraint applies to the drive arm.
Out[74]= | 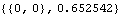 |
At T = 0.2, the driving constraint must apply a 0.65 unit moment to the drive bar to counteract the gravitational forces and the moment applied to the driven bar. A CoupleSystem object is built that seeks the value of bar2 that results in a reaction moment of 0.5 units at T = 0.2. This builds the CoupleSystem object.
Out[75]= | 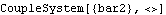 |
This solves the CoupleSystem object.
Out[76]= | 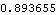 |
As with the examples given in Section 9.2, coupled systems can be built that couple multiple mechanism configurations. The conditions to be satisfied in such a system can be a mix of geometric conditions and algebraic conditions based on reaction forces. 9.4.3 Dynamic SolutionsAn option for SetCouple. In all of the preceding examples, SetCouple has been called with the default setting for the Solution option, Solution -> Automatic. SetCouple automatically upgrades the Solution setting to Velocity when first-order terms are encountered in the equations, or to Acceleration when second-order terms are encountered. SetCouple chooses the Static setting if Lagrange multipliers are encountered due to reaction forces in the equations.
However, SetCouple does not automatically choose the Kinematic or Dynamic settings for Solution unless first- or second-order terms and Lagrange multiplier terms appear in the equations, even though a dynamic solution (that includes inertial forces) may be desired. In the following example a CoupleSystem object is built with exactly the same inputs as in the previous example, but the Solution -> Dynamic option causes inertial forces to be included, resulting in a different solution. Here is the reaction that the driving constraint applies to the drive arm, including dynamic forces.
Out[78]= | 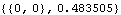 |
With dynamic forces included, the reaction moment at the drive bar is reduced to only 0.48 units at T = 0.2. A new CoupleSystem object is built that seeks the value of bar2 that results in a reaction moment of 0.5 units at T = 0.2, the same reaction moment that was sought in the previous example. This builds the CoupleSystem object with a dynamic formulation.
Out[79]= | 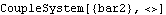 |
Note that the resulting length of the drive bar is quite different than was calculated using only static forces. This solves the CoupleSystem object.
Out[80]= | 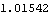 |
9.4.4 Dependent TimeA combined form of SetCouple and SolveCouple. FindTime options. FindTime is essentially a special combined form of the SetCouple and SolveCouple functions that accepts only one condition to be satisfied, and considers time to be the only new dependent variable. This seeks the time at which the reaction on the drive bar is equal to 8.
Out[81]= | 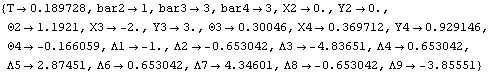 |
FindTime automatically pulls its initial guesses from the current default initial guess list LastSolve[] and it updates the initial guess list with the new solution that it finds. This shows that the specified condition has been met.
Out[82]= |  |
This clears the parameters list.
|