ElementMeshRegionProduct[mesh1,mesh2]
represents the Cartesian product of the ElementMesh mesh1 and mesh2.


ElementMeshRegionProduct
ElementMeshRegionProduct[mesh1,mesh2]
represents the Cartesian product of the ElementMesh mesh1 and mesh2.
Details and Options
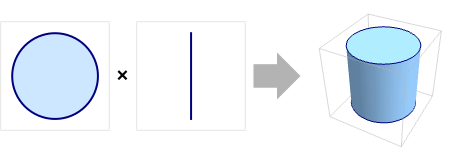
- ElementMeshRegionProduct is also known as outer product region or region extrusion.
- ElementMeshRegionProduct[mesh1,mesh2] represents the region
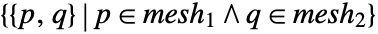 .
. - The embedding dimension of the product region is the sum of embedding dimensions, and the geometric dimension is the sum of geometric dimensions.
- The highest product dimension supported is 3.
- ElementMeshRegionProduct has the same options as ToElementMesh, with the following additions and changes:
-
"RegionMarkerFunction" None specify region markers
Examples
open all close allBasic Examples (2)
Create an ElementMesh:
Compute the ElementMesh region product:
Visualize the region product mesh:
Create three ElementMesh instances:
Compute the ElementMesh region product:
Scope (1)
Create two ElementMesh instances:
Extrude the first ElementMesh with the second by forming a region product:
Options (2)
"RegionMarkerFunction" (2)
Create a marker association and a region member function:
Define a region marker function:
Create ElementMesh that is used in each direction:
Compute the ElementMesh region product:
Inspect the "MeshElementMarkerUnion" of the generated mesh:
Visualize the region product mesh with the region markers:
Create a marker association and a region member function:
Define a region marker function:
Create ElementMesh that is used in each direction:
Compute the ElementMesh region product:
Applications (2)
Create a 2D graded mesh from a product of two 1D graded meshes:
Create a 1D graded mesh with a "Central" point distribution:
Create a second 1D graded mesh with a "Central" point distribution and 50 elements:
Visualize the region product of the anisotropic mesh:
Create a third 1D graded mesh with a "BothEnds" point distribution, 50 elements and an endpoint distance of 1/200:
Tech Notes
Related Guides
Text
Wolfram Research (2021), ElementMeshRegionProduct, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/ElementMeshRegionProduct.html (updated 2023).
CMS
Wolfram Language. 2021. "ElementMeshRegionProduct." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2023. https://reference.wolfram.com/language/FEMDocumentation/ref/ElementMeshRegionProduct.html.
APA
Wolfram Language. (2021). ElementMeshRegionProduct. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/ElementMeshRegionProduct.html
BibTeX
@misc{reference.wolfram_2025_elementmeshregionproduct, author="Wolfram Research", title="{ElementMeshRegionProduct}", year="2023", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/ElementMeshRegionProduct.html}", note=[Accessed: 03-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_elementmeshregionproduct, organization={Wolfram Research}, title={ElementMeshRegionProduct}, year={2023}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/ElementMeshRegionProduct.html}, note=[Accessed: 03-March-2026]}