NDSolve`FEM`
NDSolve`FEM`

EvaluateOnElementMesh

EvaluateOnElementMesh[{x1,…},f,mesh]

形式的なパラメータ{x1,…}に依存する f がElementMesh mesh 上で評価されたInterpolatingFunctionを返す．

EvaluateOnElementMesh[{x1,…},{f1,…},mesh]

複数の式{f1,…}を同じメッシュ mesh 上で評価する．

EvaluateOnElementMesh[{x1,…},f,mesh]

mesh に複数の材料領域がある場合にDiscontinuousInterpolatingFunctionを返す．

詳細とオプション

  • EvaluateOnElementMeshは，InterpolatingFunctionとDiscontinuousInterpolatingFunctionのいずれかを返す．
  • 補間関数は，解 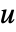がメッシュのノードの値である方程式系 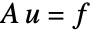を解くことによって作成される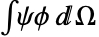．の弱形式の離散化された行列で，形状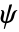関数 と検定関数 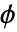を持つ．
  • EvaluateOnElementMeshは決して 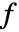をメッシュノードで評価しないが，メッシュ要素の統合点で評価する．
  • EvaluateOnElementMeshは以下のオプションを持つ．
  • "DiscontinuousInterpolation" Automatic自動的に不連続性を処理することをオフにする
    "ExtrapolationHandler" Automatic外挿がどのように処理されるかを指定する
    "MarkerPriority" Automatic境界での動作を指定する

例題

すべて開くすべて閉じる

例  (2)

パッケージをロードする：

円板の要素メッシュを作成する：

メッシュ上で関数を評価する：

解を可視化する：

複数の材料のElementMeshを作成して可視化する：

材料領域で不連続である関数を作成する：

メッシュ上で不連続関数を評価する：

不連続補間関数を可視化する：

オプション  (3)

"DiscontinuousInterpolation"  (1)

複数の材料マーカーを含むメッシュが与えられる場合には，不連続補間がデフォルトである．不連続補間を行いたくない場合には，"DiscontinuousInterpolation" Falseのオプションでオフにすることができる．

複数の領域を持つメッシュを生成して可視化する：

材料領域で不連続である関数を作成する：

メッシュ上で不連続関数を評価する：

メッシュ上で不連続関数を評価するが，InterpolatingFunctionを生成する：

"ExtrapolationHandler"  (1)

デフォルトで，EvaluateOnElementMeshを通して生成されたInterpolatingFunctionあるいはDiscontinuousInterpolatingFunctionは，警告メッセージを発して外挿を行うことによって，外挿を処理する．この動作は変更可能である．

メッシュ上で関数を評価する：

領域外でInterpolatingFunctionについてクエリを行う：

領域外のクエリにIndeterminateを返す外挿ハンドラを含むInterpolatingFunctionを構築する：

領域外のクエリについて外挿し，警告メッセージを発しない外挿ハンドラを含むInterpolatingFunctionを構築する：

外挿の処理についての詳細は，ElementMeshInterpolationを参照されたい．

"MarkerPriority"  (1)

マーカーの優先度を指定することによって，どの値が材料の境界領域で使われるかを制御することができる．以下の1Dのメッシュ例について考える：

メッシュはマーカー10と20を含む：

マーカー10の要素すべてに–1の値，そしてその他の要素に1の値を与える関数を書く：

不連続補間関数を作成する：

関数を可視化する：

不連続関数を の境界領域点で評価する：

不連続補間関数のマーカー優先度を調べると，マーカー10がマーカー20に優先することが分かる．これは，マーカー10に関連付けられた値がマーカー20に関連付けられた値よりも高い優先権を持つことを意味する：

境界領域での値は，マーカーの優先権を変更することによって設定できる：

これでマーカーの優先度が変更された：

境界領域の位置 における値がマーカー20に関連付けられた値に変更された：

全体的なプロットは同じように見えるが，境界領域での値のみが変更された：

アプリケーション  (1)

EvaluateOnElementMeshを使って不連続の勾配を計算することができる．

複数の材料メッシュを作成する：

不連続係数を持つ偏微分方程式を設定する：

境界条件を設定する：

方程式を解く：

解を可視化する：

メッシュ上の解の勾配を求める：

ベクトル場を可視化する：

Wolfram Research (2024), EvaluateOnElementMesh, Wolfram言語関数， https://reference.wolfram.com/language/FEMDocumentation/ref/EvaluateOnElementMesh.html.

テキスト

Wolfram Research (2024), EvaluateOnElementMesh, Wolfram言語関数， https://reference.wolfram.com/language/FEMDocumentation/ref/EvaluateOnElementMesh.html.

CMS

Wolfram Language. 2024. "EvaluateOnElementMesh." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/FEMDocumentation/ref/EvaluateOnElementMesh.html.

APA

Wolfram Language. (2024). EvaluateOnElementMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/EvaluateOnElementMesh.html

BibTeX

@misc{reference.wolfram_2024_evaluateonelementmesh, author="Wolfram Research", title="{EvaluateOnElementMesh}", year="2024", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/EvaluateOnElementMesh.html}", note=[Accessed: 03-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_evaluateonelementmesh, organization={Wolfram Research}, title={EvaluateOnElementMesh}, year={2024}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/EvaluateOnElementMesh.html}, note=[Accessed: 03-December-2024 ]}