EvaluateOnElementMesh[{x1,…},f,mesh]
returns an InterpolatingFunction where f depending on formal parameters {x1,…} was evaluated on the ElementMesh mesh.
EvaluateOnElementMesh[{x1,…},{f1,…},mesh]
evaluates multiple expressions {f1,…} on the same mesh mesh.
EvaluateOnElementMesh[{x1,…},f,mesh]
returns a DiscontinuousInterpolatingFunction if mesh has multiple material regions.


EvaluateOnElementMesh
EvaluateOnElementMesh[{x1,…},f,mesh]
returns an InterpolatingFunction where f depending on formal parameters {x1,…} was evaluated on the ElementMesh mesh.
EvaluateOnElementMesh[{x1,…},{f1,…},mesh]
evaluates multiple expressions {f1,…} on the same mesh mesh.
EvaluateOnElementMesh[{x1,…},f,mesh]
returns a DiscontinuousInterpolatingFunction if mesh has multiple material regions.
Details and Options
- EvaluateOnElementMesh either returns an InterpolatingFunction or a DiscontinuousInterpolatingFunction.
- The interpolating function is created by solving a system of equations
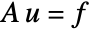 where the solution
where the solution 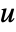 is the values at the nodes of the mesh.
is the values at the nodes of the mesh. 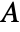 is the discretized matrix of the weak form of
is the discretized matrix of the weak form of 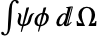 , with shape function
, with shape function 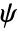 and test function
and test function 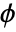 .
. - EvaluateOnElementMesh never evaluates
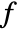 at mesh nodes, but evaluates at the integration point of the mesh elements.
at mesh nodes, but evaluates at the integration point of the mesh elements. - EvaluateOnElementMesh has the following options:
-
"DiscontinuousInterpolation" Automatic switch off automatic discontinuity handling "ExtrapolationHandler" Automatic specify how extrapolation is handled "MarkerPriority" Automatic speficy behavior at the boundary
Examples
open all close allBasic Examples (2)
Generate an element mesh for a disk:
Evaluate the function ![]() on the mesh:
on the mesh:
Create and visualize a multi-material ElementMesh:
Create a function that is discontinuous in the material region:
Options (3)
"DiscontinuousInterpolation" (1)
Discontinuous interpolation is the default, if a mesh with several material markers is given. In case discontinuous interpolation is not wanted, it can be turned off with the option "DiscontinuousInterpolation" False.
Generate and visualize a mesh with multiple regions:
Create a function that is discontinuous in the material region:
Evaluate the discontinuous function on the mesh:
Evaluate the discontinuous function on the mesh but generate an InterpolatingFunction:
"ExtrapolationHandler" (1)
By default, the InterpolatingFunction or the DiscontinuousInterpolatingFunction generated through EvaluateOnElementMesh will handle extrapolation by giving a warning message and performing an extrapolation. This behavior can be changed.
Evaluate the function ![]() on the mesh:
on the mesh:
Query the InterpolatingFunction outside of its domain:
Construct an InterpolatingFunction with an extrapolation handler that returns Indeterminate for queries outside the domain:
Construct an InterpolatingFunction with an extrapolation handler that extrapolates and does not give a warning message for queries outside the domain:
More information on extrapolation handling can be found in ElementMeshInterpolation.
"MarkerPriority" (1)
Specifying a marker priority allows you to control which value will be used at the material interface. Consider this 1D example mesh:
The mesh has markers 10 and 20:
Write a function that will give a value of –1 for all elements with marker 10 and a value of 1 for all other elements:
Create a discontinuous interpolating function:
Evaluate the discontinuous function at the interface position at ![]() :
:
By inspecting the marker priority of the discontinuous interpolating function, you can see that the marker 10 precedes the marker 20. This means values associated with marker 10 will have a higher precedence than the values associated with marker 10:
The value at the interface can be set by changing the precedence of the markers:
Now, the marker priority has changed:
The value at the interface position ![]() has changed to the value associated with marker 20:
has changed to the value associated with marker 20:
The overall plot looks the same, as only the value at the interface has changed:
Possible Issues (1)
Computing a gradient of an InterpolatingFunction with EvaluateOnElementMesh can be problematic.
Set up the partial differential equation with a discontinuous coefficient:
Find the gradient of the solution on the mesh:
Visualize the gradient in the ![]() direction along the
direction along the ![]() axis:
axis:
A continuous value would be expected. This comes up because the gradient was computed on the interpolating function directly and then evaluated on the element mesh. A better approach is to first convert the interpolating function to a DiscontinuousInterpolatingFunction:
Compute the gradient on the DiscontinuousInterpolatingFunction:
Visualize the gradient in the ![]() direction along the
direction along the ![]() axis at
axis at ![]() :
:
Visualize the gradient in the ![]() direction along the
direction along the ![]() axis at
axis at ![]() :
:
The value of the constant at ![]() can be changed by specifying a different "MarkerPriority":
can be changed by specifying a different "MarkerPriority":
Related Guides
Text
Wolfram Research (2024), EvaluateOnElementMesh, Wolfram Language function, https://reference.wolfram.com/language/FEMDocumentation/ref/EvaluateOnElementMesh.html.
CMS
Wolfram Language. 2024. "EvaluateOnElementMesh." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/FEMDocumentation/ref/EvaluateOnElementMesh.html.
APA
Wolfram Language. (2024). EvaluateOnElementMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/EvaluateOnElementMesh.html
BibTeX
@misc{reference.wolfram_2025_evaluateonelementmesh, author="Wolfram Research", title="{EvaluateOnElementMesh}", year="2024", howpublished="\url{https://reference.wolfram.com/language/FEMDocumentation/ref/EvaluateOnElementMesh.html}", note=[Accessed: 10-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_evaluateonelementmesh, organization={Wolfram Research}, title={EvaluateOnElementMesh}, year={2024}, url={https://reference.wolfram.com/language/FEMDocumentation/ref/EvaluateOnElementMesh.html}, note=[Accessed: 10-March-2026]}