HexahedronElement
HexahedronElement[{{i11,…,i18},…,{in1,…,in8}}]
インシデント{ik1,…ik8}を持つ n 個の線形六面体要素 ek を表す.
HexahedronElement[{{i11,…,i120},…,{in1,…,in20}}]
インシデント{ik1,…,ik20}を持つ n 個の二次六面体要素 ek を表す.
HexahedronElement[{e1,…,en},{m1,…,mn}]
n 個の六面体要素 ek と n 個の整数マーカー mk を表す.
詳細とオプション
- HexahedronElementを使ってElementMesh内の六面体のメッシュ要素を表す.
- HexahedronElementは,ToElementMeshあるいはToBoundaryMeshへの入力として使うことができる.
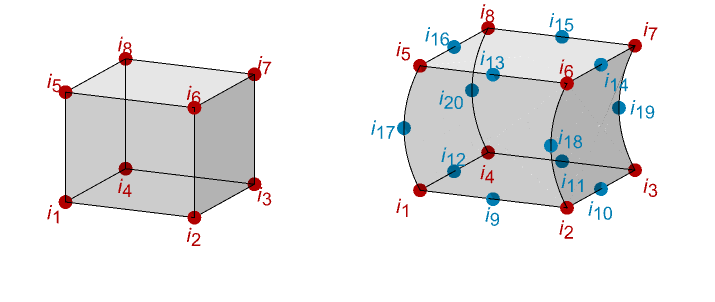
- インシデント ik,j は,空間座標の配列に指標を付ける整数である.ek={ik1,…}が参照する座標は, k
 番目の三角形のノードである.
番目の三角形のノードである. - 最初の3つのインシデント ik1 は,ik8 までは常に頂点である.
- 二次三角要素については,次の12個のインシデントは,曲がっている可能性のある辺の中間のノードである.
- 線形要素は,次数1の要素であり,二次要素は,次数2の要素である.
- HexahedronElement[{e1,…,en}]では,すべての要素 ek が同じ次数でなければならない.
- HexahedronElement[{e1,…,en}]の六面体は,共通のノード,辺,面を共有するが,お互いが交差したり,それ自身と交差したりすることがあってはならない.
- 線形と二次の六面体についてノードが示されている.
- HexahedronElementについては,面のインシデントは,要素の内側から見た場合に反時計回りでなければならない.要素{i1,…,i8}は,面のインシデント{i1,i2,i3,i4},{i8,i7,i6,i5},{i1,i5,i6,i2},{i2,i6,i7,i3},{i3,i7,i8,i4},{i4,i8,i5,i1}を6つの面について持つ.
- 六面体要素は,有限要素法では,セレンディピティ要素として知られている.
例題
すべて開くすべて閉じる一般化と拡張 (4)
テキスト
Wolfram Research (2014), HexahedronElement, Wolfram言語関数, https://reference.wolfram.com/language/FEMDocumentation/ref/HexahedronElement.html.
CMS
Wolfram Language. 2014. "HexahedronElement." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/FEMDocumentation/ref/HexahedronElement.html.
APA
Wolfram Language. (2014). HexahedronElement. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/FEMDocumentation/ref/HexahedronElement.html