FourierSeries`
FourierSeries`
NFourierTrigSeries
NFourierTrigSeries[expr,t,k]
gives a numerical approximation to the order n Fourier trigonometric series expansion of expr, where expr is a periodic function of t with period 2π.
Details and Options
- To use NFourierTrigSeries, you first need to load the Fourier Series Package using Needs["FourierSeries`"].
- The numerical approximation to the order n Fourier exponential series expansion of expr is by default defined to be
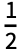c0+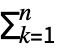
ckCos[k t]+dk Sin[k t]. - The coefficient ck is defined to be
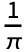NIntegrate[expr Cos[k t],{t,-π,π}] and the coefficient dk is defined to be 
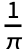NIntegrate[expr Sin[k t],{t,-π,π}]. - Different choices for the period of expr can be specified using the option FourierParameters.
- With the setting FourierParameters->{a,b}, expr is assumed to have a period of
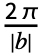, and the order n Fourier exponential series expansion computed by NFourierTrigSeries is 
(
+
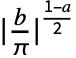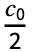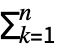ck Cos[2π b k t]+dk Sin[2π b k t]). Here, the coefficient ck is defined to be 
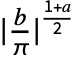NIntegrate[expr Cos[b k t],{t,-
,
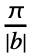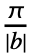}] and the coefficient dk is defined to be 
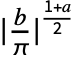NIntegrate[expr Sin[b k t],{t,-
,
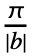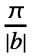}]. - The parameter b in the setting FourierParameters->{a,b} must be numeric.
- In addition to the option FourierParameters, NFourierTrigSeries can also accept the options available to NIntegrate. These options are passed directly to NIntegrate.